题目内容
已知实数x,y满足
+
=1,求x2+y2-x的最小值.
| x2 |
| 4 |
| y2 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据方程和平方关系设
,代入式子利用配方法化简,利用二次函数的性质和余弦函数的值域求出式子的最小值.
|
解答:
解:因为实数x,y满足
+
=1,所以设
,θ为参数,
则x2+y2-x=4cos2θ+2sin2θ-2cosθ=2+2cos2θ-2cosθ
=2+2(cosθ-
)2-
=2(cosθ-
)2+
,
当(cosθ-
)2=0时,式子取到最小值是
,
所以x2+y2-x的最小值是
.
| x2 |
| 4 |
| y2 |
| 2 |
|
则x2+y2-x=4cos2θ+2sin2θ-2cosθ=2+2cos2θ-2cosθ
=2+2(cosθ-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当(cosθ-
| 1 |
| 2 |
| 3 |
| 2 |
所以x2+y2-x的最小值是
| 3 |
| 2 |
点评:本题考查椭圆方程的点的坐标参数设法,余弦函数的值域,二次函数的性质,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
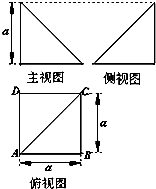 四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )
四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A,其三视图如图所示,则四棱锥P-ABCD的表面积为( )A、(2
| ||
| B、2a2 | ||
C、(1+
| ||
D、(2+
|