题目内容
非零向量
,
满足|
|=1,|
|=2,|
-
|=2,则|
+
|= .
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| 2b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的平方即为模的平方,计算即可得到所求值.
解答:
解:|
|=1,|
|=2,|
-
|=2,
即为(
-
)2=4,
2+
2-2
•
=4,
即有
•
=
,
则|
+
|=
=
=
=
.
故答案为:
.
| a |
| b |
| a |
| b |
即为(
| a |
| b |
| a |
| b |
| a |
| b |
即有
| a |
| b |
| 1 |
| 2 |
则|
| a |
| 2b |
(
|
|
=
1+4×4+4×
|
| 19 |
故答案为:
| 19 |
点评:本题考查平面向量的数量积的性质,考查向量的平方即为模的平方,考查运算能力,属于基础题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
数列{(-1)n•n}的前2015项的和S2015为( )
| A、-2013 | B、-1008 |
| C、2013 | D、1008 |
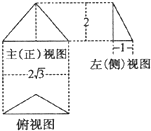 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的四个表面中,面积的最大值为