题目内容
4．已知p：x＞1，q：（x-2）（x-a）＜0（a≠2），若a=3，则p是q的必要不充分条件；若p既不是q的充分条件，也不是q必要条件，则a的取值范围是（-∞，1）．分析 ①a=3，对于q：（x-2）（x-3）＜0，解得2＜x＜3．即可判断出p与q的关系．
②a＞2时，对于q：（x-2）（x-a）＜0，解得2＜x＜a．可得p是q的必要不充分条件条件．舍去．a＜2时，对于q：（x-2）（x-a）＜0，解得a＜x＜2．对a分类讨论：a＜1，1≤a＜2，即可的判断出关系．
解答 解：①a=3，对于q：（x-2）（x-3）＜0，解得2＜x＜3．则p是q的必要不充分条件．
②a＞2时，对于q：（x-2）（x-a）＜0，解得2＜x＜a．则p是q的必要不充分条件条件．舍去．
a＜2时，对于q：（x-2）（x-a）＜0，解得a＜x＜2．
若a＜1，则p既不是q的充分条件，也不是q必要条件，满足条件．
若1≤a＜2，则p是q的必要不充分条件条件．舍去．
综上可得：a的取值范围是（-∞，1）．
故答案为：必要不充分条件，（-∞，1）．
点评 本题考查了不等式的解法、分类讨论方法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
精英口算卡系列答案
相关题目
13．设x，y满足约束条件$\left\{\begin{array}{l}x+y-2≥0\\ x-y+1≥0\\ x≤3\end{array}\right.$，若z=mx+y的最小值为-3，则m的值为（ ）
| A． | -9 | B． | $-\frac{7}{3}$ | C． | $-\frac{2}{3}$ | D． | $\frac{2}{3}$ |
20．已知函数f（x）=ax2+bx+c，且a＞b＞c，a+b+c=0，集合A={m|f（m）＜0}，则（ ）
| A． | 任意m∈A，都有f（m+3）＞0 | B． | 任意m∈A，都有f（m+3）＜0 | ||
| C． | 存在m∈A，都有f（m+3）=0 | D． | 存在m∈A，都有f（m+3）＜0 |
9．
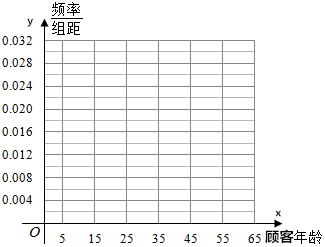某电商在6月18日之后，随机抽取100名顾客进行回访，按顾客的年龄分成6组，得到如下频数分布表：
（1）在表中作出这些数据的频率分布直方图；
（2）根据（1）中的频率分布直方图，求这100名顾客年龄的平均数；
（3）用分层抽样的方法从这100名顾客中抽取25人，再从抽取的25人中随机抽取2人，求年龄在[25，35）内的顾客人数X的分布列与数学期望．
某电商在6月18日之后，随机抽取100名顾客进行回访，按顾客的年龄分成6组，得到如下频数分布表：| 顾客年龄 | [5，15） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65] |
| 频数 | 4 | 24 | 32 | 20 | 16 | 4 |
（2）根据（1）中的频率分布直方图，求这100名顾客年龄的平均数；
（3）用分层抽样的方法从这100名顾客中抽取25人，再从抽取的25人中随机抽取2人，求年龄在[25，35）内的顾客人数X的分布列与数学期望．