题目内容
16.设数列{an}满足${a_1}=\frac{3}{8}$,且对任意的n∈N*,满足${a_{n+2}}-{a_n}≤{3^n},{a_{n+4}}-{a_n}≥10×{3^n}$,则a2017=$\frac{{{3^{2017}}}}{8}$.分析 对任意的n∈N*,满足${a_{n+2}}-{a_n}≤{3^n},{a_{n+4}}-{a_n}≥10×{3^n}$,可得10×3n≤(an+4-an+2)+(an+2-an)≤3n+2+3n=10×3n.an+4-an=10×3n.利用a2017=(a2017-a2013)+(a2013-a2009)+…+(a5-a1)+a1与等比数列的求和公式即可得出.
解答 解:∵对任意的n∈N*,满足${a_{n+2}}-{a_n}≤{3^n},{a_{n+4}}-{a_n}≥10×{3^n}$,
∴10×3n≤(an+4-an+2)+(an+2-an)≤3n+2+3n=10×3n.
∴an+4-an=10×3n.
∴a2017=(a2017-a2013)+(a2013-a2009)+…+(a5-a1)+a1
=10×(32013+32009+…+3)+$\frac{3}{8}$
=10×$\frac{3×(8{1}^{504}-1)}{81-1}$+$\frac{3}{8}$=$\frac{{3}^{2017}}{8}$.
故答案为:$\frac{{{3^{2017}}}}{8}$.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、累加求和方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
7.已知α为第二象限角,sin(α+$\frac{π}{4}$)=$\frac{\sqrt{2}}{10}$,则tanα的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $-\frac{4}{3}$ | D. | -3 |
1.已知双曲线与椭圆$\frac{x^2}{9}+\frac{y^2}{25}=1$的焦点相同,且它们的离心率的乘积等于$\frac{8}{5}$,则此双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{y^2}{4}-\frac{x^2}{12}=1$ | C. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
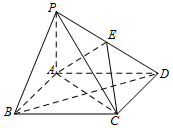 如图,在四棱锥P-ABCD中,PA=AB=$\frac{1}{2}$AD=2,PB=2$\sqrt{2}$,PA⊥AD,底面ABCD为平行四边形,∠ADC=60°,E为PD的中点.
如图,在四棱锥P-ABCD中,PA=AB=$\frac{1}{2}$AD=2,PB=2$\sqrt{2}$,PA⊥AD,底面ABCD为平行四边形,∠ADC=60°,E为PD的中点.