题目内容
设数列{an},an≠0,a1=
,若以an-1,an为系数的二次方程:an-1x2+anx-1=0(n≥2,n∈N*)都有两个不同的根α,β满足3α-αβ+3β+1=0
(1)求证:{an-
}为等比数列;
(2)求{an}的通项公式并求前n项和Sn.
| 5 |
| 6 |
(1)求证:{an-
| 1 |
| 2 |
(2)求{an}的通项公式并求前n项和Sn.
(1)∵3(α+β)-αβ+1=0,
∴依题意,得3
-
=1(n≥2),
∴3an-1=an-1(n≥2),
∴3(an-
)=an-1-
(n≥2),
∴{an-
}是公比为
,首项为
-
=
的等比数列;
(2)由(1)知,an-
=
•(
)n-1=(
)n,
∴an=
+(
)n,
∴Sn=a1+a2+…+an
=(
+
)+(
+(
)2)+…+(
+(
)n)
=
+
=
-
.
∴依题意,得3
| an |
| an-1 |
| 1 |
| an-1 |
∴3an-1=an-1(n≥2),
∴3(an-
| 1 |
| 2 |
| 1 |
| 2 |
∴{an-
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)由(1)知,an-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴an=
| 1 |
| 2 |
| 1 |
| 3 |
∴Sn=a1+a2+…+an
=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
=
| n |
| 2 |
| ||||
1-
|
=
| n+1 |
| 2 |
| 1 |
| 2×3n |

练习册系列答案
相关题目
 的前
的前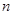 项和为
项和为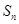 ,且
,且 是
是 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: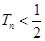 .
.