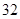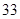题目内容
数列 的前
的前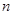 项和为
项和为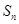 ,且
,且 是
是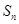 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前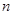 项和为
项和为 ,证明:
,证明: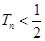 .
.
 的前
的前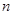 项和为
项和为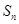 ,且
,且 是
是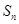 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.(1)求数列
 、
、 的通项公式;
的通项公式;(2)设
 ,数列
,数列 的前
的前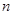 项和为
项和为 ,证明:
,证明: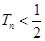 .
.(1)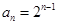 ,
, ;(2)证明见解析.
;(2)证明见解析.
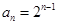 ,
, ;(2)证明见解析.
;(2)证明见解析.试题分析:(1)由题中所给条件得
 ,即
,即 ,这是前
,这是前 项和
项和 与项
与项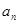 的关系,我们可以利用
的关系,我们可以利用 把此式转化为数列的项的递推式
把此式转化为数列的项的递推式 ,从而知数列
,从而知数列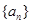 是等比数列,通项易得,这样等差数列的
是等比数列,通项易得,这样等差数列的 ,
, ,由基本量法可求得等差数列
,由基本量法可求得等差数列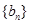 的通项公式;(2)数列
的通项公式;(2)数列 是由等差数列相邻两项相乘后取倒数所得,其前
是由等差数列相邻两项相乘后取倒数所得,其前 项和应该用裂项相消法求得,而当求得
项和应该用裂项相消法求得,而当求得 后,所要证的不等式就显而易见成立了.
后,所要证的不等式就显而易见成立了.(1)∵
 是
是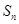 和
和 的等差中项,∴
的等差中项,∴
当
 时,
时, ,∴
,∴
当
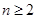 时,
时,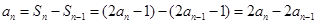 , ∴
, ∴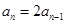 ,即
,即 
∴数列
 是以
是以 为首项,
为首项,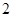 为公比的等比数列,∴
为公比的等比数列,∴ ,
,
设
 的公差为
的公差为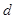 ,
, ,
, ,∴
,∴ ∴
∴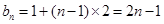 - 6分
- 6分(2)
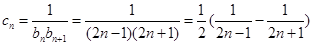
∴

∵
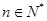 ,∴
,∴ 12分
12分 项和
项和 与项
与项 的关系,求通项公式,等差数列、等比数列通项公式;(2)裂项相消法求和与不等式。
的关系,求通项公式,等差数列、等比数列通项公式;(2)裂项相消法求和与不等式。
练习册系列答案
相关题目
 }中,
}中, ,且
,且
 ,
, 的值;
的值; 是数列
是数列 前
前 项和,且
项和,且 ,对
,对 ,总有
,总有 ,则
,则 。
。 依它的前10项的规律,则
依它的前10项的规律,则 _.
_.  }满足
}满足  ,
, ,
, , ...,
, ...,  ,...,是首项为1,公比为2的等比数列,那么
,...,是首项为1,公比为2的等比数列,那么 .其中满足性质“对任意的正整数n,
.其中满足性质“对任意的正整数n, ≤an+1都成立”的数列有________(写出所有满足条件的序号).
≤an+1都成立”的数列有________(写出所有满足条件的序号). 行中从左至右第
行中从左至右第 与第
与第 个数的比为
个数的比为 ,
,