题目内容
已知f(x)是定义在(0,+∞)上的增函数,当n∈N*时,有f(n)∈N*,f[f(n)]=3n,则f(1)+f(2)+f(3)+f(4)= .
考点:函数单调性的性质
专题:函数的性质及应用
分析:结合题设条件,利用列举法一一验证,能够求出f(1)、f(2)、f(3)、f(4)的值,从而求得f(1)+f(2)+f(3)+f(4)的值.
解答:
解:若f(1)=1,则f(f(1))=f(1)=1,与条件f(f(n))=3n矛盾,故不成立.
若f(1)=3,则f(f(1))=f(3)=3,进而f(f(3))=f(3)=9,与前式矛盾,故不成立.
若f(1)=n(n>3),则f(f(1))=f(n)=3,与f(x)单调递增矛盾.
所以只剩f(1)=2.验证之:f(f(1))=f(2)=3,
进而f(f(2))=f(3)=6,
进而f(f(3))=f(6)=9,
由函数的单调性,f(4)=7,f(5)=8,
∴f(1)+f(2)+f(3)+f(4)=2+3+6+7=18,
故答案为:18.
若f(1)=3,则f(f(1))=f(3)=3,进而f(f(3))=f(3)=9,与前式矛盾,故不成立.
若f(1)=n(n>3),则f(f(1))=f(n)=3,与f(x)单调递增矛盾.
所以只剩f(1)=2.验证之:f(f(1))=f(2)=3,
进而f(f(2))=f(3)=6,
进而f(f(3))=f(6)=9,
由函数的单调性,f(4)=7,f(5)=8,
∴f(1)+f(2)+f(3)+f(4)=2+3+6+7=18,
故答案为:18.
点评:本题考查函数值的求法,解题时要认真审题,仔细解答,注意列举法的合理运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=f(x)是定义域为R的偶函数.当x≥0时,f(x)=
若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是( )
|
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
已知log2m=2.013,log2n=1.013,则
等于( )
| n |
| m |
| A、2 | ||
B、
| ||
| C、10 | ||
D、
|
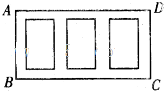 如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道,已知三块绿化区的总面积为600平方米,求该矩形区域ABCD占地面积的最小值.
如图,某广场要划定一矩形区域ABCD,并在该区域内开辟出三块形状大小相同的小矩形绿化区,这三块绿化区四周和绿化区之间分别设有2米宽和1米宽的走道,已知三块绿化区的总面积为600平方米,求该矩形区域ABCD占地面积的最小值.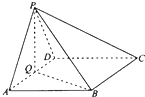 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.