题目内容
甲袋和乙袋装有大小相同的红球和白球，已知甲袋中有m个球，乙袋中有2m个球，从甲袋中摸出1个球为红球的概率为
，从乙袋中摸出1个球为红球的概率为P．
（Ⅰ）若m=10，从甲袋中红球的个数；
（Ⅱ）设P=
，若从甲、乙两袋中各自有放回地模球，从甲袋中模1次，从乙袋中摸2次，每次摸出1个球，设ξ表示摸出红球的总次数，求ξ的分布列和数学期望．
| 1 |
| 5 |
（Ⅰ）若m=10，从甲袋中红球的个数；
（Ⅱ）设P=
| 1 |
| 5 |
考点：离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题：概率与统计
分析：（Ⅰ）甲袋中有10个球，从甲袋中摸出1个球为红球的概率为
，由此能嫠出甲袋中红球的个数．
（Ⅱ）由题设知ξ=0，1，2，3，分别求出相应在的概率，由此能求出ξ的分布列和数学期望．
| 1 |
| 5 |
（Ⅱ）由题设知ξ=0，1，2，3，分别求出相应在的概率，由此能求出ξ的分布列和数学期望．
解答：
解：（Ⅰ）∵甲袋中有10个球，从甲袋中摸出1个球为红球的概率为
，
∴甲袋中红球的个数为10×
=2．
（Ⅱ）由题设知ξ=0，1，2，3，
P(ξ=0)=(
)3=
，
P(ξ=1)=
(
)(
)2=
，
P(ξ=2)=
(
)2(
)=
，
P（ξ=3）=（
）3=
，
∴ξ的分布列为：
E(ξ)=0×
+1×
+2×
+3×
=
．
| 1 |
| 5 |
∴甲袋中红球的个数为10×
| 1 |
| 5 |
（Ⅱ）由题设知ξ=0，1，2，3，
P(ξ=0)=(
| 4 |
| 5 |
| 64 |
| 125 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 48 |
| 125 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 12 |
| 125 |
P（ξ=3）=（
| 1 |
| 5 |
| 1 |
| 125 |
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
| 3 |
| 5 |
点评：本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，是中档题．
练习册系列答案
相关题目
已知1，a1，a2，9四个实数成等差数列，1，b1，b2，b3，9五个数成等比数列，则b2（a2-a1）等于（ ）
| A、8 | ||
| B、-8 | ||
| C、±8 | ||
D、
|
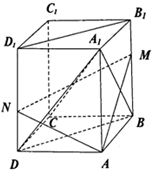如图，长方体ABCD-A1B1C1D1中，点M，N分别在BB1，DD1上，且AM⊥A1B，AN⊥A1D．