题目内容
已知bn=
,求数列的前n项和Sn<
的最大n的值.
| 2 |
| n2+n |
| 5 |
| 3 |
考点:数列的求和
专题:等差数列与等比数列
分析:由bn=
=2(
-
),利用裂项求和法求解数列的前n项和Sn<
的最大n的值.
| 2 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
| 5 |
| 3 |
解答:
解:∵bn=
=2(
-
),
∴Sn=2(1-
+
-
+…+
)
=2(1-
)=
∵数列的前n项和Sn<
,
∴由
<
,得6n<5n+5,解得n<5.
∵nn∈N*,∴Sn<
的最大n的值为4.
| 2 |
| n2+n |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
=2(1-
| 1 |
| n+1 |
| 2n |
| n+1 |
∵数列的前n项和Sn<
| 5 |
| 3 |
∴由
| 2n |
| n+1 |
| 5 |
| 3 |
∵nn∈N*,∴Sn<
| 5 |
| 3 |
点评:本题考查数列的前n项和Sn<
的最大n的值的求法,是基础题,解题时要认真审题,注意裂项求和法的合理运用.
| 5 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
,则f(f(-2))=( )
|
| A、2 | B、1 | C、-2 | D、-1 |


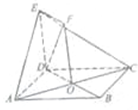 如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=
如图,O为正方形ABCD的中心,四边形ODEF是平行四边形,且平面ODEF⊥平面ABCD,AD=2,DE=