题目内容
20.在抛物线y=x2上求一点M,使它到直线y=2x-4的距离最短,则M点的坐标为(1,1).分析 求导数,利用导数的几何意义,求出切点坐标,即可求出M点的坐标.
解答 解:∵y=x2,
∴y′=2x,
令y′=2x=2,可得x=1,y=1,
即M(1,1)到直线y=2x-4的距离最短,
故答案为:(1,1).
点评 本题考查抛物线方程,考查导数的几何意义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
5.甲、乙两人连续6年对农村甲鱼养殖业(产量)进行调查,提供了两个方面的信息,甲调查表明,每个甲鱼池平均出产量从第一年1万只上升到第六年的2万只.
乙调查表明,甲鱼池的个数由第一年的30个减少到第6年的10个.
(1)求第2年全县产甲鱼的总数;
(2)到第6年这个县甲鱼养殖业的规模比第1年是扩大了还是缩小了?说明理由.
(3)求哪一年的规模最大?说明原因.
| 年 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 每池产量 | 1万只 | 1.2万只 | 1.4万只 | 1.6万只 | 1.8万只 | 2万只 |
| 年 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 鱼池个数 | 30个 | 26个 | 22个 | 18个 | 14个 | 10个 |
(2)到第6年这个县甲鱼养殖业的规模比第1年是扩大了还是缩小了?说明理由.
(3)求哪一年的规模最大?说明原因.
11.若两个函数的图象有一个公共点,并在该点处的切线相同,就说这两个函数有why点.已知函数f(x)=lnx和g(x)=em•ex有why点,则m所在的区间为( )
| A. | $({-2,-\frac{3}{2}})$ | B. | $({-\frac{3}{2},-1})$ | C. | $({-\frac{5}{2},-2})$ | D. | $({-1,-\frac{1}{3}})$ |
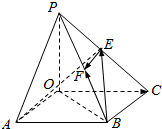 如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.
如图,四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=$\overrightarrow{c}$,E,F分别是PC和PB的中点,用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{BF}$、$\overrightarrow{BE}$、$\overrightarrow{AE}$、$\overrightarrow{EF}$.