题目内容
15．设f（x），g（x）都是定义在R上的函数，若函数y=f（g（x））-x有零点，则函数g（f（x））不可能是（ ）| A． | x2-$\frac{1}{5}$ | B． | x2+$\frac{1}{5}$ | C． | x2+x-$\frac{1}{5}$ | D． | x2+x+$\frac{1}{5}$ |
分析 由函数y=f（g（x））-x有零点可判断g（f（x））=x有解，从而分别代入判断即可．
解答 解：∵函数y=f（g（x））-x有零点，
∴方程f（g（x））=x有解，
∴g（f（g（x）））=g（x），
∴g（f（x））=x有解，
若g（f（x））=x2-$\frac{1}{5}$，
则可判断x2-$\frac{1}{5}$=x有解，故成立；
若g（f（x））=x2+$\frac{1}{5}$，
则可判断x2+$\frac{1}{5}$=x有解，故成立；
若g（f（x））=x2+x-$\frac{1}{5}$，
则可判断x2+x-$\frac{1}{5}$=x有解，故成立；
若g（f（x））=x2+x+$\frac{1}{5}$，
则可判断x2+x+$\frac{1}{5}$=x无解，故不成立；
故选：D．
点评 本题考查了复合函数的性质的应用及方程的根与函数的零点的关系应用．
练习册系列答案
相关题目
5．长方体ABCD-A1B1C1D1中，AA1=3，AD=4，AB=5，则直线BD1与平面ABCD所成的角的正弦值是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{{3\sqrt{2}}}{10}$ | C． | $\frac{3}{{\sqrt{34}}}$ | D． | $\frac{5}{{\sqrt{34}}}$ |
3．
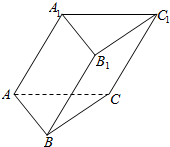如图，在三棱柱ABC-A1B1C1中，各棱长均相等，且∠A1AB=∠A1AC=∠BAC=60°，则AB1与底面ABC所成角的正弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，各棱长均相等，且∠A1AB=∠A1AC=∠BAC=60°，则AB1与底面ABC所成角的正弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{\sqrt{2}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{1}{2}$ |