题目内容
3.已知各项均为正数的等比数列{an}的前n项和为Sn,且S3=14,a3=8,则a6=( )| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
分析 由题意可得$\left\{\begin{array}{l}{\frac{{a}_{1}(1-{q}^{3})}{1-q}=14}\\{{a}_{1}{q}^{2}=8}\end{array}\right.$,解得a1=2,q=2,即可求出a6.
解答 解:∵S3=14,a3=8,
∴$\left\{\begin{array}{l}{\frac{{a}_{1}(1-{q}^{3})}{1-q}=14}\\{{a}_{1}{q}^{2}=8}\end{array}\right.$,
解得a1=2,q=2,
∴a6=a1q5=2×32=64,
故选:C
点评 本题考查了等比数列的前n项和以及等比数列的通项公式,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
14.正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
11.若复数z=$\frac{1-3i}{1+i}$(i为虚数单位),则|z+1|=( )
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
18.在△ABC中,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{3}|{\overrightarrow{AB}-\overrightarrow{AC}}|$,$|{\overrightarrow{AB}}|=|{\overrightarrow{AC}}|=3$,则$\overrightarrow{CB}•\overrightarrow{CA}$的值为( )
| A. | 3 | B. | -3 | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
13.在棱长为4的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM和CN所成的角的余弦值是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
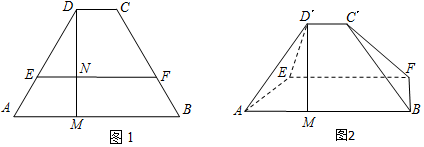
 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,BD=2AD=8,AB=4$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,BD=2AD=8,AB=4$\sqrt{5}$.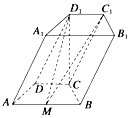 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.