题目内容
4.在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2-b2=3actanB,则角B的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
分析 根据题意,利用余弦定理化简a2+c2-b2=3actanB,再由同角的三角函数关系,即可求出sinB的值,再根据B∈(0,π)求得B的值.
解答 解:△ABC中,a2+c2-b2=3actanB,
由余弦定理得2accosB=3actanB,
∴2cosB•cosB=3sinB,
即2(1-sin2B)=3sinB,
整理得2sin2B+3sinB-2=0,
解得sinB=$\frac{1}{2}$或sinB=-2(不合题意,舍去);
又B∈(0,π),
∴B的值为$\frac{π}{6}$或$\frac{5π}{6}$.
故选:C.
点评 本题考查了余弦定理以及同角三角函数关系的应用问题,是基础题.

练习册系列答案
相关题目
14.正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
16.过点P(1,1)且倾斜角为45°的直线被圆(x-2)2+(y-1)2=2所截的弦长是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
13.在棱长为4的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM和CN所成的角的余弦值是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
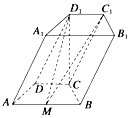 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.