题目内容
19.已知角α(0°≤α<360°)终边上一点的坐标为(sin215°,cos215°),则α=( )| A. | 215° | B. | 225° | C. | 235° | D. | 245° |
分析 利用诱导公式,任意角的三角函数的定义,求得α的值.
解答 解:∵角α(0°≤α<360°)终边上一点的坐标为(sin215°,cos215°),
由三角函数定义得cosα=sin215°=cos235°,sinα=cos215°=sin235°,∴α=235°,
故选:C.
点评 本题主要考查诱导公式,任意角的三角函数的定义,属于基础题.

练习册系列答案
相关题目
7.为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
( I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.05 |
| [60,70) | a | 0.20 |
| [70,80) | 35 | b |
| [80,90) | 25 | 0.25 |
| [90,100) | 15 | 0.15 |
| 合计 | 100 | 1.00 |
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
4.设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时,$f(x)=\frac{1}{6}{x^2}-\frac{1}{2}a{x^2}+x$,在x∈(-1,2)上为“凸函数”,则函数f(x)在(-1,2)上结论正确的是( )
| A. | 既有极大值,也有极小值 | B. | 有极大值,没有极小值 | ||
| C. | 没有极大值,有极小值 | D. | 既无极大值,也没有极小值 |
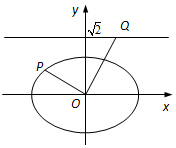 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.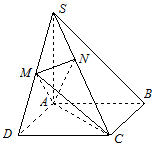 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.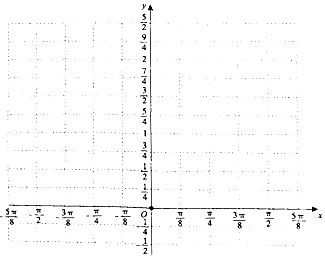 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.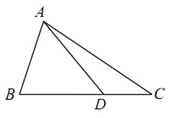 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.