题目内容
9.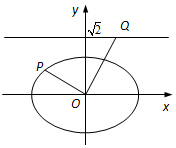 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,焦点到相应准线的距离为1.(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线$y=\sqrt{2}$于点Q,求$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}$的值.
分析 (1)由已知条件可得$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,$\frac{a^2}{c}-c=1$,然后求解椭圆的方程.
(2)由题意知OP的斜率存在.当OP的斜率为0时,求解结果;当OP的斜率不为0时,设直线OP方程为y=kx.联立方程组,推出$O{P^2}=\frac{{2{k^2}+2}}{{2{k^2}+1}}$.OQ2=2k2+2.然后求解即可.
解答 解:(1)由题意得,$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,$\frac{a^2}{c}-c=1$,…2分
解得$a=\sqrt{2}$,c=1,b=1.
所以椭圆的方程为$\frac{x^2}{2}+{y^2}=1$. …4分
(2)由题意知OP的斜率存在.
当OP的斜率为0时,$OP=\sqrt{2}$,$OQ=\sqrt{2}$,所以$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}=1$. …6分
当OP的斜率不为0时,设直线OP方程为y=kx.
由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\;\\ y=kx\;\end{array}\right.$得(2k2+1)x2=2,解得${x^2}=\frac{2}{{2{k^2}+1}}$,所以${y^2}=\frac{{2{k^2}}}{{2{k^2}+1}}$,
所以$O{P^2}=\frac{{2{k^2}+2}}{{2{k^2}+1}}$. …9分
因为OP⊥OQ,所以直线OQ的方程为$y=-\frac{1}{k}x$.
由$\left\{\begin{array}{l}y=\sqrt{2}\;\\ y=-\frac{1}{k}x\end{array}\right.$得$x=-\sqrt{2}k$,所以OQ2=2k2+2. …12分
所以$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}=\frac{{2{k^2}+1}}{{2{k^2}+2}}+\frac{1}{{2{k^2}+2}}=1$.
综上,可知$\frac{1}{{O{P^2}}}+\frac{1}{{O{Q^2}}}=1$. …14分.
点评 本题考查椭圆的简单性质的应用,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{5}$ |
| A. | 215° | B. | 225° | C. | 235° | D. | 245° |