题目内容
10.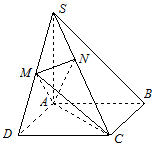 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=2,点M是SD的中点,AN⊥SC,且交SC于点N.(Ⅰ) 求证:SB∥平面ACM;
(Ⅱ) 求点C到平面AMN的距离.
分析 (Ⅰ)连结BD交AC于E,连结ME,推导出ME∥SB,由此能证明SB∥平面ACM.
(Ⅱ)推导出CN为点C到平面AMN的距离,由此能求出点C到平面AMN的距离.
解答 证明:(Ⅰ)连结BD交AC于E,连结ME.
∵ABCD是正方形,∴E是BD的中点.
∵M是SD的中点,∴ME是△DSB的中位线.
∴ME∥SB. …(3分)
又∵ME?平面ACM,SB?平面ACM,
∴SB∥平面ACM. …(5分)
解:(Ⅱ)由条件有DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,∴AM⊥DC.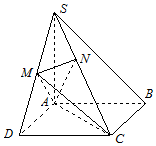
又∵SA=AD,M是SD的中点,∴AM⊥SD.
∴AM⊥平面SDC.∴SC⊥AM.…(8分)
由已知SC⊥AN,∴SC⊥平面AMN.
于是CN⊥面AMN,则CN为点C到平面AMN的距离 …(9分)
在Rt△SAC中,$SA=2,AC=2\sqrt{2},SC=\sqrt{S{A^2}+A{C^2}}=2\sqrt{3}$,
于是$A{C^2}=CN•SC⇒CN=\frac{{4\sqrt{3}}}{3}$
∴点C到平面AMN的距离为$\frac{{4\sqrt{3}}}{3}$. …(12分)
点评 本题考查线面平行的证明,考查点到直线的距离求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
1.直线l:4x-5y=20经过双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一个焦点和虚轴的一个端点,则C的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{5}$ |
5.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右焦点分别为F1,F2,直线l经过点F1及虚轴的一个端点,且点F2到直线l的距离等于实半轴的长,则双曲线的离心率为( )
| A. | $\frac{{1+\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{4}$ | C. | $\sqrt{\frac{{1+\sqrt{5}}}{2}}$ | D. | $\frac{{\sqrt{3+\sqrt{5}}}}{2}$ |
2.《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其意思为:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内投豆子,则落在其内切圆内的概率是( )
| A. | $\frac{3π}{10}$ | B. | $\frac{π}{20}$ | C. | $\frac{3π}{20}$ | D. | $\frac{π}{10}$ |
19.已知角α(0°≤α<360°)终边上一点的坐标为(sin215°,cos215°),则α=( )
| A. | 215° | B. | 225° | C. | 235° | D. | 245° |