题目内容
4.设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时,$f(x)=\frac{1}{6}{x^2}-\frac{1}{2}a{x^2}+x$,在x∈(-1,2)上为“凸函数”,则函数f(x)在(-1,2)上结论正确的是( )| A. | 既有极大值,也有极小值 | B. | 有极大值,没有极小值 | ||
| C. | 没有极大值,有极小值 | D. | 既无极大值,也没有极小值 |
分析 根据函数恒成立,得出m的值,利用函数单调性得出结果.
解答 解:$g(x)=f'(x)=\frac{1}{2}{x^2}-ax+1$,
由已知得g′(x)=x-a<0,当x∈(-1,2)时恒成立,
故a≥2,又已知a≤2,故a=2,
此时由f′(x)=0,得:x1=2-$\sqrt{2}$,x2=2+$\sqrt{2}$∉(-1,2),
当x∈(-1,2-$\sqrt{2}$)时,f′(x)>0;当x∈(2-$\sqrt{2}$,2)时,f′(x)<0,
所以函数f(x)在(-1,2)有极大值,没有极小值,
故选:B.
点评 本题主要考查导数和函数知识及利用导数判断函数单调性,属于基础知识,基本运算的考查.

练习册系列答案
相关题目
19.已知角α(0°≤α<360°)终边上一点的坐标为(sin215°,cos215°),则α=( )
| A. | 215° | B. | 225° | C. | 235° | D. | 245° |
13.我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、…、《辑古算经》等算经10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部名著中选择2部作为“数学文化”校本课程学习内容,则所选2部名著中至少有一部是魏晋南北朝时期的名著的概率为( )
| A. | $\frac{14}{15}$ | B. | $\frac{13}{15}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
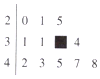 在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )
在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )