题目内容
9.设数列{an}的前n项和为Sn,且Sn=-1+2an(Ⅰ)求{an}的通项公式;
(Ⅱ)若bn=log2an+1,且数列{bn}的前n项和为Tn,求$\frac{1}{{T}_{1}}+\frac{1}{{T}_{2}}$+…+$\frac{1}{{T}_{n}}$.
分析 (Ⅰ)由数列递推式求出首项,进一步得当n≥2时,Sn-1=-1+2an-1,与原递推式联立可得an=2an-1(n≥2),即{an}是2为公比,1为首项的等比数列,再由等比数列的通项公式求得{an}的通项公式;
(Ⅱ)把数列通项公式代入bn=log2an+1,求出数列{bn}的前n项和为Tn,再由裂项相消法求$\frac{1}{{T}_{1}}+\frac{1}{{T}_{2}}$+…+$\frac{1}{{T}_{n}}$.
解答 解:(Ⅰ)由已知,有Sn=-1+2an,①
当n=1时,a1=-1+2a1,即a1=1.
当n≥2时,Sn-1=-1+2an-1,②
①-②得an=Sn-Sn-1=2an-2an-1,即an=2an-1(n≥2).
∴{an}是2为公比,1为首项的等比数列,即${a}_{n}={2}^{n-1}$.
(Ⅱ)由(Ⅰ),得${b}_{n}=lo{g}_{2}{a}_{n+1}=lo{g}_{2}{2}^{n}=n$,
∴${T}_{n}=1+2+…+n=\frac{n(n+1)}{2}$.
∴$\frac{1}{{T}_{1}}+\frac{1}{{T}_{2}}+…+\frac{1}{{T}_{n}}=\frac{2}{1×2}+\frac{2}{2×3}+\frac{2}{3×4}+…+$$\frac{2}{n(n+1)}$
=$2(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n}-\frac{1}{n+1})$=2$(1-\frac{1}{n+1})=\frac{2n}{n+1}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的前n项和,是中档题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 215° | B. | 225° | C. | 235° | D. | 245° |
| A. | ∅ | B. | {0} | C. | {1} | D. | {0,1} |
| A. | $\frac{7}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{4}$ |
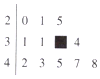 在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )
在如图所示一组数据的茎叶图中,有一个数字被污染后而模糊不清,但曾计算得该组数据的极差与中位数之和为61,则被污染的数字为( )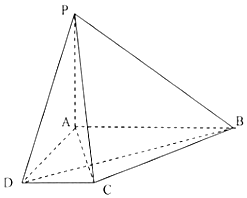 如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.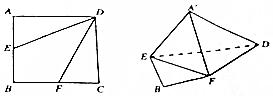 如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,在边长为4的正方形ABCD中,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.