题目内容
12.若x,y满足约束条件$\left\{{\begin{array}{l}{2x+y-2≥0}\\{x-y+2≥0}\\{4x-y-4≤0}\end{array}}\right.$,若z=ax-y有最小值6,则实数a等于5.分析 作出可行域,变形目标函数,分类讨论并数形结合平移直线可得结论.
解答 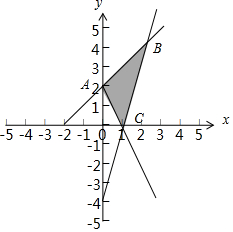 解:x,y满足约束条件$\left\{{\begin{array}{l}{2x+y-2≥0}\\{x-y+2≥0}\\{4x-y-4≤0}\end{array}}\right.$,
解:x,y满足约束条件$\left\{{\begin{array}{l}{2x+y-2≥0}\\{x-y+2≥0}\\{4x-y-4≤0}\end{array}}\right.$,
所对应的可行域(如图△ABC),A(0,2),B(2,4),C(1,0),
z=ax-y有最小值6,
变形目标函数可得y=ax-z,
当a>0时,直线经过点B(2,4)时,直线截距最大值,
目标函数z取最小值,故2a-4=6,解得a=5,
当a<0时,没有符合条件的可行域的点,
给答案为:5.
点评 本题考查简单线性规划,准确作图并数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
2.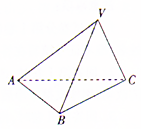 如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
 如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )
如图所示,三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形,侧面VAC与底面ABC垂直,若以垂直于平面VAC的方向作为正视图的方向,垂直于平面ABC的方向为俯视图的方向,已知其正视图的面积为2$\sqrt{3}$,则其侧视图的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
20.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点为F1、F2,其中一条渐近线方程为y=3x,过点F2作x轴的垂线与双曲线的一个交点为M,若△MF1F2的面积为18$\sqrt{10}$,则双曲线的方程为( )
| A. | x2-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{9}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{2}$=1 |
4.已知集合$A=\left\{{x\left|{y=lgx}\right.}\right\},B=\left\{{y|y=\sqrt{x-1}}\right\}$,则A∪B=( )
| A. | [1,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | (0,+∞) |
1.对函数f(x),在使f(x)≥M成立的所有常数M中,我们把M的最大值叫做函数f(x)的下确界.现已知定义在R上的偶函数f(x)满足f(1-x)=f(1+x),当x∈[0,1]时,f(x)=-3x2+2,则f(x)的下确界为( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
1.已知椭圆C1和双曲线C2焦点相同,且离心率互为倒数,F1,F2是它们的公共焦点,P是椭圆和双曲线在第一象限的交点,若∠F1PF2=60°,则椭圆C1的离心率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
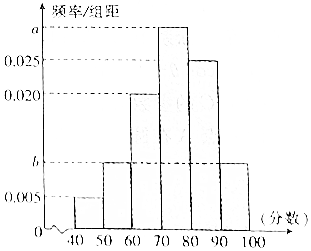 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.