题目内容
已知数列{an}的前n项和Sn满足:Sn=
(1-an)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=nSn,求数列{bn}的前n项和Tn.
| 1 |
| 2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=nSn,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据an与Sn的关系,即可求数列{an}的通项公式;
(Ⅱ)求出bn,利用错位相减法,即可求出数列{bn}的前n项和Tn.
(Ⅱ)求出bn,利用错位相减法,即可求出数列{bn}的前n项和Tn.
解答:
解:(Ⅰ)∵S1=
(1-a1)=a1,
∴a1=
,
当n≥2时,an=Sn-Sn-1=-
an+
an-1,an=
an-1,
即{an}是以
为首项,
为公比的等比数列.
∴an=(
)n;
(Ⅱ)Sn=
(1-an)=
-
(
)n,bn=nSn=
-
(
)n,
Tn=b1+b2+b3+…+bn=
(1+2+3+…+n)-
(
+
+
+…+
)=
-
(
+
+
+…+
),
令Mn=
+
+
+…+
①,
Mn=
+
+
+…+
②
①-②得:
Mn=
+
+
+…+
-
=
-
=
-
,
∴Mn=
-
,
∴Tn=
+
.
| 1 |
| 2 |
∴a1=
| 1 |
| 3 |
当n≥2时,an=Sn-Sn-1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
即{an}是以
| 1 |
| 3 |
| 1 |
| 3 |
∴an=(
| 1 |
| 3 |
(Ⅱ)Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| n |
| 2 |
| n |
| 2 |
| 1 |
| 3 |
Tn=b1+b2+b3+…+bn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 32 |
| 3 |
| 33 |
| n |
| 3n |
| n(n+1) |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 32 |
| 3 |
| 33 |
| n |
| 3n |
令Mn=
| 1 |
| 3 |
| 2 |
| 32 |
| 3 |
| 33 |
| n |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 2 |
| 33 |
| 3 |
| 34 |
| n |
| 3n+1 |
①-②得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| n |
| 3n |
| ||||
1-
|
| n |
| 3n+1 |
| 1 |
| 2 |
| 2n+3 |
| 2•3n+1 |
∴Mn=
| 3 |
| 4 |
| 2n+3 |
| 4•3n |
∴Tn=
| 2n2+2n-3 |
| 8 |
| 2n+3 |
| 8•3n |
点评:本题主要考查数列的通项公式,考查数列求和,要求熟练掌握错位相减法进行求和,考查学生的运算能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定.空气质量指数越高,代表空气污染越严重:
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定.空气质量指数越高,代表空气污染越严重: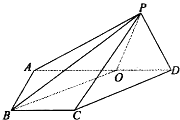 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.