题目内容
数列{an}满足a1=1，an+4an-1=0（n≥2），则a2与a4的等比中项是（ ）
| A、4 | B、±4 | C、16 | D、±16 |
考点：数列递推式
专题：等差数列与等比数列
分析：利用递推思想求出a2与a4，由此能求出a2与a4的等比中项．
解答：
解：∵数列{an}满足a1=1，an+4an-1=0（n≥2），
∴an=-4an-1，
∴a2=-4×1=-4，
a3=-4×（-4）=16，
a4=-4×16=-64，
∴a2与a4的等比中项是：±
=±16．
故选：D．
∴an=-4an-1，
∴a2=-4×1=-4，
a3=-4×（-4）=16，
a4=-4×16=-64，
∴a2与a4的等比中项是：±
| (-4)×(-64) |
故选：D．
点评：本题考查a2与a4的等比中项的求法，是中档题，解题时要注意递推思想的合理运用．
练习册系列答案
相关题目
按如图程序框图，若输出结果为S=42，则判断框内应补充的条件为（ ）
| A、i＞3 | B、i＞5 |
| C、i＞7 | D、i＞9 |
下列命题错误的是（ ）
| A、命题“若m≤0，则方程x2+x+m=0有实数根”的逆否命题为：“若方程x2+x+m=0无实数根，则m＞0” |
| B、“x=2”是“x2-x-2=0”的充分不必要条件 |
| C、若命题“p且q”为假命题，则命题“p”与命题“q”中必有一真一假 |
| D、对于命题p：存在x∈R，x2+x+1＜0，则非p：对任意x∈R，x2+x+1≥0 |
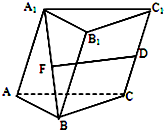
在三棱柱ABC-A1B1C1中，D是CC1的中点，F是A1B的中点，且
=α
+β
，则（ ）
| DF |
| AB |
| AC |
A、α=
| ||
B、α=-
| ||
C、α=1，β=-
| ||
D、α=-1，β=
|
（x2+
）6的展开式中x3的系数是（ ）
| 2 |
| x |
| A、20 | B、160 |
| C、240 | D、60 |
已知0＜α＜
＜β＜π，tan
=
，cos（α-β）=
，则β的值为（ ）
| π |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
| ||
| 10 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设x=30.5，y=log32，z=cos2，则（ ）
| A、z＜y＜x |
| B、z＜x＜y |
| C、y＜z＜x |
| D、x＜z＜y |
已知f（x）=
，则f（log27）=（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|