题目内容
已知f（x）=
，则f（log27）=（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：分段函数的应用
专题：函数的性质及应用
分析：根据函数的周期性以及分段函数的表达式，结合对数的运算法则，代入即可得到结论．
解答：
解：当x＞0时，f（x）=f（x-1），
∵2＜log27＜3，
∴-1＜log27-3＜0，
则f（log27）=f（log27-3）=f（log2
）=(
)log2
=2log2
=
，
故选：C
∵2＜log27＜3，
∴-1＜log27-3＜0，
则f（log27）=f（log27-3）=f（log2
| 7 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
| 8 |
| 7 |
| 8 |
| 7 |
故选：C
点评：本题主要考查函数值的计算，根据分段函数的表达式以及函数的周期性进行转化是解决本题的关键．
练习册系列答案
相关题目
数列{an}满足a1=1，an+4an-1=0（n≥2），则a2与a4的等比中项是（ ）
| A、4 | B、±4 | C、16 | D、±16 |
不等式
＞1的解集为（ ）
| 2 |
| x-1 |
| A、{x|x＞3} |
| B、{x|1＜x＜3} |
| C、{x|x＜3} |
| D、{x|x＜3或x＞1} |
若x＞y＞1，0＜a＜1，那么下列各式中正确的是（ ）
| A、x-a＞y-a |
| B、logax＞logay |
| C、ax＜ay |
| D、ax＞ay |
设全集U=R，A={x|x（x-2）＜0}，B={x|y=ln（1-x）＜0}，则图中阴影部分表示的集合为（ ）
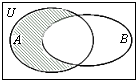
| A、{x|0＜x≤1} |
| B、{x|1≤x＜2} |
| C、{x|x≥1} |
| D、{x|x≤1} |
下列命题中，真命题是（ ）
| A、空间不同三点确定一个平面 |
| B、空间两两相交的三条直线确定一个平面 |
| C、两组对边相等的四边形是平行四边形 |
| D、和同一直线都相交的三条平行线在同一平面内 |
函数y=（
）x+2+1（a＞0，a≠1）图象必经过点（ ）
| 1 |
| a |
| A、（-1，1） |
| B、（-1，2） |
| C、（-2，1） |
| D、（-2，2） |
已知关于x的二次函数y=ax2+bx+c（a＞0）的图象经过点C（0，2），且与x轴交于不同的两点A、B，点A的坐标是（1，0）．