题目内容
已知等比数列{an}的首项a1=
,公比q=
,设bn+2=3log
an(n∈N*),数列{cn}满足cn=anbn.
(Ⅰ)求{bn}的通项公式;
(Ⅱ)求数列{cn}的前n项和Sn;
(Ⅲ)对任意n∈N*,cn≤m2-m-
恒成立,求m的取值范围.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(Ⅰ)求{bn}的通项公式;
(Ⅱ)求数列{cn}的前n项和Sn;
(Ⅲ)对任意n∈N*,cn≤m2-m-
| 1 |
| 2 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由题意知an=(
)n,所以bn+2=3log
an=3n,由此能求出bn=3n-2.
(Ⅱ)由cn=(3n-2)•(
)n.利用错位相减法能求出数列{cn}的前n项和Sn.
(3)由已知条件求出cn取最大值
,所以对任意n∈N*,cn≤m2-m-
恒成立,等价国土m2-m-
≥
,由此能求出m的取值范围.
| 1 |
| 4 |
| 1 |
| 4 |
(Ⅱ)由cn=(3n-2)•(
| 1 |
| 4 |
(3)由已知条件求出cn取最大值
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:(Ⅰ)∵等比数列{an}的首项a1=
,公比q=
,
∴an=(
)n,
∴bn+2=3log
an=3n,
∴bn=3n-2.
(Ⅱ)∵an=(
)n,bn=3n-2,∴cn=(3n-2)•(
)n.
∴Sn=1×
+4×(
)2+…+(3n-2)×(
)n,
Sn=1×(
)2+4×(
)2+…+(3n-2)×(
)n+1,
两式相减,得
Sn=
+3×[(
)2+(
)3+…+(
)n]-(3n-2)×(
)n+1
=
+
-(3n-2)×(
)n+1
=
-
-(3n-2)×(
)n+1,
∴Sn=
-
×(
)n+1.
(3)∵Cn+1-Cn=(3n+1)×(
)n+1-(3n-2)×(
)n=9(1-n)×(
)n+1.
当n=1时,c2=c1=
,
n≥2时,cn+1<cn,
∴cn取最大值
,
∵对任意n∈N*,cn≤m2-m-
恒成立,
∴m2-m-
≥
,解得m≥
,或m≤
.
| 1 |
| 4 |
| 1 |
| 4 |
∴an=(
| 1 |
| 4 |
∴bn+2=3log
| 1 |
| 4 |
∴bn=3n-2.
(Ⅱ)∵an=(
| 1 |
| 4 |
| 1 |
| 4 |
∴Sn=1×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
两式相减,得
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| ||||
1-
|
| 1 |
| 4 |
=
| 1 |
| 2 |
| 1 |
| 4n |
| 1 |
| 4 |
∴Sn=
| 2 |
| 3 |
| 12n+8 |
| 3 |
| 1 |
| 4 |
(3)∵Cn+1-Cn=(3n+1)×(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
当n=1时,c2=c1=
| 1 |
| 4 |
n≥2时,cn+1<cn,
∴cn取最大值
| 1 |
| 4 |
∵对任意n∈N*,cn≤m2-m-
| 1 |
| 2 |
∴m2-m-
| 1 |
| 2 |
| 1 |
| 4 |
1+
| ||
| 2 |
1+
| ||
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查实数的取值范围的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
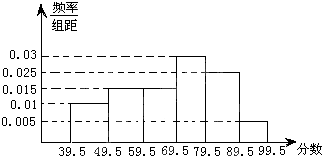 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
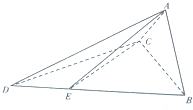 如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体A-BCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE= 如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.求证:
如图,四棱锥P-ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.求证: