题目内容
已知圆C的圆心在坐标原点,且过点M(1 ,
).
(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线x+y-4=0的距离的最小值;
(3)若直线l与圆C相切于点M,求直线l的方程.
| 3 |
(1)求圆C的方程;
(2)已知点P是圆C上的动点,试求点P到直线x+y-4=0的距离的最小值;
(3)若直线l与圆C相切于点M,求直线l的方程.
考点:直线与圆相交的性质,圆的标准方程,圆的切线方程
专题:直线与圆
分析:(1)由题意可得圆C的半径r=|OM|的值,再根据原点为圆心,可得圆的方程.
(2)求出圆心到直线x+y-4=0的距离d,则点P到直线x+y-4=0的距离的最小值为d-r,计算可得结果.
(3)先求出直线l的斜率为
的值,再由点斜式求得直线l的方程,化简可得结果.
(2)求出圆心到直线x+y-4=0的距离d,则点P到直线x+y-4=0的距离的最小值为d-r,计算可得结果.
(3)先求出直线l的斜率为
| -1 |
| KOM |
解答:
解:(1)由题意可得圆C的半径r=|OM|=
=2,再根据原点为圆心,
可得圆的方程为 x2+y2=4.
(2)已知点P是圆C上的动点,圆心到直线x+y-4=0的距离d=
=2
,
故点P到直线x+y-4=0的距离的最小值为d-r=2
-2.
(3)若直线l与圆C相切于点M(1,
),故直线l的斜率为
=
=-
,
由点斜式求得直线l的方程为 y-
=-
(x-1),即 x+
y-4=0.
12+(
|
可得圆的方程为 x2+y2=4.
(2)已知点P是圆C上的动点,圆心到直线x+y-4=0的距离d=
| |0+0-4| | ||
|
| 2 |
故点P到直线x+y-4=0的距离的最小值为d-r=2
| 2 |
(3)若直线l与圆C相切于点M(1,
| 3 |
| -1 |
| KOM |
| -1 | ||||
|
| ||
| 3 |
由点斜式求得直线l的方程为 y-
| 3 |
| ||
| 3 |
| 3 |
点评:本题主要考查求圆的标准方程的方法,直线和圆的位置关系,点到直线的距离公式,用点斜式求直线的方程,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
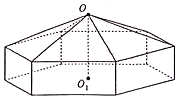 一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.
一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.