Question

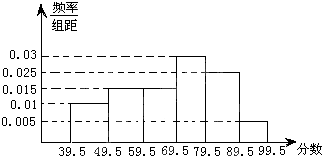如图，从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如图所示，观察图形，回答下列问题：
（1）79.5～89.5这一组的频率、频数分别是多少？
（2）估计这次环保知识竞赛的及格率（60分及以上为及格）
（3）从60名学生中抽取4名，再从中抽2名，求恰好有1名是及格的概率．

Answer 1

考点：古典概型及其概率计算公式,频率分布直方图

专题：概率与统计

分析：（1）先求[79.5，89.5）这一组的矩形的高，然后根据直方图中的各个矩形的面积代表了频率，频数=样本容量×频率，进行求解；
（2）先根据直方图中的各个矩形的面积代表了频率求出60分及以上的频率，从而估计总体这次环保知识竞赛的及格率．
（3）从60名学生中抽取4名，其中及格学生人数为4×0.75=3人，不及格人数为1人，再从这4人中抽2名，能求出恰好有1名是及格的概率．

解答： 解：（1）[79.5，89.5）这一组的矩形的高为0.025，
直方图中的各个矩形的面积代表了频率，
则[79.5，89.5）这一组的频率=0.025×10=0.25，
频数=0.25×60=15，
[79.5，89.5）这一组的频数为15、频率0.25；
（2）60分及以上的频率=（0.015+0.03+0.025+0.005）×10=0.75，
估计这次环保知识竞赛的及格率为75%．
（3）从60名学生中抽取4名，其中及格学生人数为4×0.75=3人，不及格人数为4×(1-

3

4

)=1人，
再从这4人中抽2名，恰好有1名是及格的概率：
p=

C 1 3 C 1 1

C 2 4

=

1

2

．

点评：本题考查频率分布直方图的相关知识，直方图中的各个矩形的面积代表了频率，所以各个矩形面积之和为1，以及频数=样本容量×频率，属于基础题．