题目内容
1.观察下列式子:$\sqrt{1×2}<2$,$\sqrt{1×2}+\sqrt{2×3}<\frac{9}{2}\sqrt{1×2}+\sqrt{2×3}+\sqrt{3×4}<8$,$\sqrt{1×2}+\sqrt{2×3}+\sqrt{3×4}+\sqrt{4×5}<\frac{25}{2}$,…,根据以上规律,第n个不等式是$\sqrt{1×2}+\sqrt{2×3}+…+\sqrt{n×(n+1)}<\frac{{{{(n+1)}^2}}}{2}$.
分析 根据所给不等式,即可得出结论.
解答 解:根据所给不等式可得$\sqrt{1×2}+\sqrt{2×3}+…+\sqrt{n×(n+1)}<\frac{{{{(n+1)}^2}}}{2}$.
故答案为:$\sqrt{1×2}+\sqrt{2×3}+…+\sqrt{n×(n+1)}<\frac{{{{(n+1)}^2}}}{2}$.
点评 本题考查归纳推理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
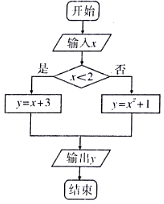
16.设x∈[0,3],执行如图所示的程序框图,从输出的结果中随机取一个数a,则“a≤5”的概率为( )

| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{5}{7}$ |
13.已知函数f(x)=x3+ax+1的图象在点(1,f(1))处的切线过点(2,7),则a=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
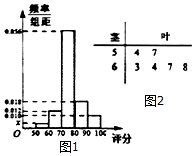 某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.
某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.