题目内容

11．已知四面体ABCD，AB=4，AC=AD=6，∠BAC=∠BAD=60°，∠CAD=90°，则该四面体外接球半径为2$\sqrt{5}$．

分析 作出图形，利用勾股定理，求出四面体外接球半径．

解答 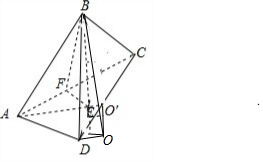解：如图所示，O′为△ACD的外心，O为球心，BE⊥平面ACD，BF⊥AC，则EF⊥AC，∴AF=2，AE=2$\sqrt{2}$，BE=$\sqrt{16-8}$=2$\sqrt{2}$．
设该四面体外接球半径为R，OO′=d，则2+（2$\sqrt{2}$+d）2=d2+（3$\sqrt{2}$）2，
∴d=$\sqrt{2}$，CD=6$\sqrt{2}$，
∴R=$\sqrt{2+18}$=2$\sqrt{5}$，
故答案为：2$\sqrt{5}$．

点评 本题考查四面体外接球半径，考查勾股定理的运用，考查学生分析解决问题的能力，属于中档题．

练习册系列答案
相关题目
1．已知定义在R上的函数f（x）满足：f（x+1）=$\sqrt{f（x）{-f}^{2}（x）}+\frac{1}{2}$，数列{an}满足an=f2（n）-f（n），n∈N*，若其前n项和为-$\frac{35}{16}$，则n的值为（　　）
A．16B．17C．18D．19
2．已知双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$的左，右焦点分别为F1，F2，O为坐标原点，圆O是以F1F2为直径的圆，直线$l：\sqrt{2}x+\sqrt{3}y+t=0$与圆O有公共点．则实数t的取值范围是（　　）
A．$[{-2\sqrt{2}，2\sqrt{2}}]$B．[-4，4]C．[-5，5]D．$[{-5\sqrt{2}，5\sqrt{2}}]$
19．在平面直角坐标系xOy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率是$\frac{{\sqrt{3}}}{2}$，且直线l1：$\frac{x}{a}+\frac{y}{b}=1$被椭圆C截得的弦长为$\sqrt{5}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l1与圆D：x2+y2-6x-4y+m=0相切：
（i）求圆D的标准方程；
（ii）若直线l2过定点（3，0），与椭圆C交于不同的两点E、F，与圆D交于不同的两点M、N，求|EF|•|MN|的取值范围．
6．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≥0}\\{ax，x＜0}\end{array}\right.$若方程f（-x）=f（x）有五个不同的根，则实数a的取值范围为（　　）
A．（-∞，-e）B．（-∞，-1）C．（1，+∞）D．（e，+∞）
16．已知函数f（x）是定义域为R的奇函数，当x∈[0，1]时，f（x）=log2（x+1），则f（1-$\sqrt{2}$）=-$\frac{1}{2}$．
3．已知函数f（x）=（x2+a）ex（a是常数，e=2.71828…是自然对数的底数），曲线y=f（x）与x轴相切．
（Ⅰ）求实数a的值；
（Ⅱ）设方程f（x）=x2+x的所有根之和为S，且S∈（n，n+1），求整数n的值；
（Ⅲ）若关于x的不等式mf（x）+2x+2＜2ex在（-∞，0）内恒成立，求实数m的取值范围．
20．在条件$\left\{\begin{array}{l}{x+y-3≥0}\\{x-2y+3≤0}\\{2x-y-3≤0}\end{array}\right.$下，目标函数z=x+2y的最小值为4．
1．观察下列式子：$\sqrt{1×2}＜2$，$\sqrt{1×2}+\sqrt{2×3}＜\frac{9}{2}\sqrt{1×2}+\sqrt{2×3}+\sqrt{3×4}＜8$，$\sqrt{1×2}+\sqrt{2×3}+\sqrt{3×4}+\sqrt{4×5}＜\frac{25}{2}$，
…，根据以上规律，第n个不等式是$\sqrt{1×2}+\sqrt{2×3}+…+\sqrt{n×（n+1）}＜\frac{{{{（n+1）}^2}}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网