设全集U={1.2.3.4.5}.∁U={1}.A∩(∁UB)={3.4}.则集合B=( )A．{1.2.4.5}B．{2.4.5}C．{1.2.5}D．{2.5} 题目和参考答案——青夏教育精英家教网—

题目内容

13．设全集U={1，2，3，4，5}，∁_U（A∪B）={1}，A∩（∁_UB）={3，4}，则集合B=（　　）

A．

{1，2，4，5}

B．

{2，4，5}

C．

{1，2，5}

D．

{2，5}

分析根据全集、并集、补集与交集的定义，分析并求出集合B．

解答解：全集U={1，2，3，4，5}，∁_U（A∪B）={1}，
∴A∪B={2，3，4，5}；
又A∩（∁_UB）={3，4}，
∴3∉B，且4∉B；
∴集合B={2，5}．
故选：D．

点评本题考查了集合的定义与运算问题，是基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

4．已知α∈（0，$\frac{π}{2}$），试比较α，sinα，tanα的大小．

1．

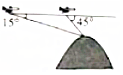航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的高度为海拔10千米，速度为180千米/小时，飞机先看到山顶的俯角为15°，经过420秒后又看到山顶的俯角为45°，则山顶的海拔高度为（取$\sqrt{2}=1.4$，$\sqrt{3}=1.7$）（　　）

	A．	命题“如果p²+q²=2，则p+q≤2”的否命题是“如果p+q＞2，则p²+q²≠2”
	B．	命题p：?x∈[0，1]，e^x≥1，命题q：?x∈R，x²+x+1＜0，则p∨q为假
	C．	若（$\sqrt{x}$-$\frac{1}{2\root{3}{x}}$）ⁿ的展开式中第四项为常数项，则n=5
	D．	“若am²＜bm²，则a＜b”的逆命题为真命题．

18．已知向量$\overrightarrow a$，$\overrightarrow{b}$为两个互相垂直的单位向量，向量$\overrightarrow c$满足$（\overrightarrow a-\overrightarrow c）•（\overrightarrow b-2\overrightarrow c）$=0，则$|\overrightarrow c{|_{max}}$=$\frac{\sqrt{5}}{2}$．

5．已知函数f（x）=$\frac{2a{x}^{2}+bx+1}{{e}^{x}}$（e为自然对数的底数）．
（1）当a=b=0时，直接写出f（x）的值域（不要求写出求解过程）；
（2）若a=$\frac{1}{2}$，求函数f（x）的单调区间；
（3）若f（1）=1，且方程f（x）=1在（0，1）内有解，求实数a的取值范围．

2．已知△ABC的面积为8，cosA=$\frac{3}{5}$，D为BC上一点，$\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$，过点D做AB，AC的垂线，垂足分别为E，F，则$\overrightarrow{DE}$•$\overrightarrow{DF}$=-$\frac{36}{25}$．

3．若实数x，y满足条件$\left\{\begin{array}{l}2x-y+1≥0\\ 2x+y-5≥0\\ x-2≤0\end{array}\right.$，则$z=\frac{4x}{3x+2y}$的最大值为（　　）

试题分类