题目内容
5.已知函数f(x)=x2+mx+4.(Ⅰ)当x∈(1,2)时,不等式f(x)<0恒成立,求实数m的取值范围;
(Ⅱ)若不等式|$\frac{f(x)-{x}^{2}}{m}$|<1的解集中的整数有且仅有1,2,求实数m的取值范围.
分析 (Ⅰ)x∈(1,2)时,不等式f(x)<0恒成立,即为$\left\{\begin{array}{l}{f(1)≤0}\\{f(2)≤0}\end{array}\right.$,解得即可,
(Ⅱ)先化简,得到|x+$\frac{4}{m}$|<1,解得-1-$\frac{4}{m}$<x<1-$\frac{4}{m}$,再根据不等式|$\frac{f(x)-{x}^{2}}{m}$|<1的解集中的整数有且仅有1,2,得到关于m的不等式组解的即可.
解答 解:(Ⅰ)x∈(1,2)时,不等式f(x)<0恒成立,
∴$\left\{\begin{array}{l}{f(1)≤0}\\{f(2)≤0}\end{array}\right.$
即$\left\{\begin{array}{l}{m+5≤0}\\{2m+4≤0}\end{array}\right.$
解得m≤-5
∴实数m的取值范围(-∞,-5],
(Ⅱ)|$\frac{f(x)-{x}^{2}}{m}$|=|x+$\frac{4}{m}$|<1,
∴-1<x+$\frac{4}{m}$<1,
∴-1-$\frac{4}{m}$<x<1-$\frac{4}{m}$,
∵不等式|$\frac{f(x)-{x}^{2}}{m}$|<1的解集中的整数有且仅有1,2,
∴0<-1-$\frac{4}{m}$≤1,且2<1-$\frac{4}{m}$≤3,
解得-4<m≤-2,
∴实数m的取值范围(-4,-2].
点评 本题考查了不等式的解法和函数的恒成立的问题,属于中档题.

练习册系列答案
相关题目
16.已知抛物线y2=20x的焦点到双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的距离为4,则该双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
13.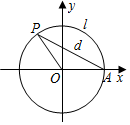 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
 如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π
如图,设点A是单位圆上的一个定点,动点P从点A出发,在圆上按逆时针方向旋转一周,点P所旋转过的弧$\widehat{AP}$的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )π| A. | 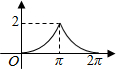 | B. | 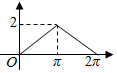 | C. |  | D. | 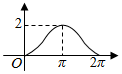 |
17.下列命题中,真命题的个数是( )
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.若正实数m、n满足3m+4n=5mn,则m+3n的最小值是( )
| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{28}{5}$ |