题目内容
已知一个直四棱柱的全面积为11，所有的棱长之和为24，求它的外接圆的表面积．
考点：球内接多面体
专题：计算题,空间位置关系与距离
分析：设出直四棱柱的长、宽、高，表示出长方体的表面积为11，十二条棱长度之和为24，然后整理可得对角线的长度，即可求它的外接圆的表面积．
解答：
解：∵设直四棱柱的长、宽、高分别为a，b，c，由题意可知，
a+b+c=6，
∴两边平方后展开得：a2+b2+c2+2ac+2ab+2bc=36，①
2ab+2bc+2ac=11…②，
由①-②可得a2+b2+c2=25，
这个直四棱柱的一条对角线长为：5，
∴直四棱柱的外接圆的半径为
，
∴直四棱柱的外接圆的表面积为4π×
=25π．
a+b+c=6，
∴两边平方后展开得：a2+b2+c2+2ac+2ab+2bc=36，①
2ab+2bc+2ac=11…②，
由①-②可得a2+b2+c2=25，
这个直四棱柱的一条对角线长为：5，
∴直四棱柱的外接圆的半径为
| 5 |
| 2 |
∴直四棱柱的外接圆的表面积为4π×
| 25 |
| 4 |
点评：本题考查直四棱柱的结构特征，面积和棱长的关系，考查计算能力及方程思想，是基础题．
练习册系列答案
相关题目
随机变量X的概率分布规律为P（X=n）=
（n=1，2，3），其中a是常数，则P（1≤X≤2）的值为（ ）
| a |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
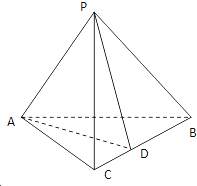如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC，点D为BC中点．