题目内容
已知
+
+
=
，|
|=2，|
|=3，|
|=
，则向量
与
的夹角为（ ）
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| 7 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由题意作差向量三角形，由余弦定理可得三角形的内角，由向量夹角的定义可得．
解答：
解：∵
+
+
=
，|
|=2，|
|=3，|
|=
，
∴它们构成如图所示的三角形OAB，
其中
=
，
=
，
=
，
在△OAB中由余弦定理可得cos∠OAB=
=
，
∴∠OAB=60°，∴向量
与
的夹角为120°
故选：D
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| 7 |
∴它们构成如图所示的三角形OAB，
其中
| OA |
| a |
| AB |
| b |
| BO |
| c |
在△OAB中由余弦定理可得cos∠OAB=
22+33-(
| ||
| 2×2×3 |
| 1 |
| 2 |
∴∠OAB=60°，∴向量
| a |
| b |
故选：D
点评：本题考查向量的夹角，涉及余弦定理，作图是解决问题的关键，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
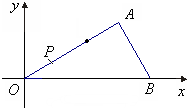如图，在平面直角坐标系中，△AOB是直角三角形，∠AOB=30°，∠A=90°，OB=12，点P在OA上，且OP=2