题目内容

若数列{an}满足an=
2an，0≤an≤1
an-1，an＞1
，且a1=
6
7
，求a2014的值．
考点：数列递推式
专题：等差数列与等比数列
分析：根据递推公式，利用递推思想求出数列的前6项，从而得到数列{an}是以5为周期的周期数列，由此能求出a2014的值．
解答： 解：∵数列{an}满足an=
2an，0≤an≤1
an-1，an＞1
，且a1=
6
7
，
∴a2=2a1=
12
7
，
a3=
12
7
-1=
5
7
，
a4=2a3=
10
7
，
a5=
10
7
-1=
3
7
，
a6=2a5=
6
7
，
∴数列{an}是以5为周期的周期数列，
又2014=402×5+4，
∴a2014=a4=
10
7
．
点评：本题考查数列的第2014项的值的求法，是基础题，解题时要认真审题，注意递推思想和数列的周期性质的合理运用．
练习册系列答案
相关题目
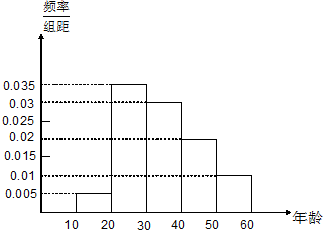某班同学利用寒假进行社会实践，对年龄段在[10，60]的人生活习惯是否符合环保理念进行调查，现随机抽取n人进行数据分析，得到如下频率分布表和频率分布直方图；
（1）求出频率分布表中n，x，y的值；
（2）现从第三、四、五组中，采用分层抽样法抽取12人参加户外环保体验活动，则从这三组中应各抽取多少人？
（3）从第三、四、五组中采用分层抽样法抽取12人参加项学习活动，从这12名中再选取3人作为领队，记这3名领队中在第三四组内人数为X，求X分布列和期望EX．
组数分组人数频率
第一组[10，20）5 
第二组[20，30） x
第三组[30，40）  
第四组[40，50）y 
第五组[50，60] 
合计 n
（1）设函数f（x）=|x-
5
2
|+|x-a|，x∈R，若关于x的不等式f（x）≥a在R上恒成立，求实数a的最大值；
（2）已知正数x，y，z满足x+2y+3z=1，求
3
x
+
2
y
+
1
z
的最小值．
已知圆过A（-1，5），B（5，5），C（6，-2）三点，求圆的方程，并画出圆形．
若将函数y=sin2x的图象向左平移φ，φ∈（0，
π
2
）个单位，再向下平移一个单位所得的函数图象过点P（
π
3
，-
1
2
），则φ的取值为（　　）
A、
π
24
B、
π
12
C、
π
6
D、
π
3
f（x）=x3+4cosx-sin
π
2
，则f′（
π
2
）=
 
．[f（
π
2
）]′=
 
．
已知sinα=
3
5
，且α是第二象限角，则cosα=
 
，tanα=
 
．
已知|
a
|=2，|
b
|=3，（
a
-
2b
）•（
2a
+
b
）=-1，则
a
与
b
的夹角为
 
．
设
a
，
b
为向量，若
a
+
b
与
a
的夹角为60°，
a
+
b
与
b
的夹角为45°，则
|
a
|
|
b
|
=（　　）
A、
3
3
B、
6
3
C、
1
2
D、
2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网