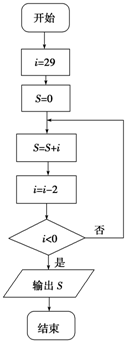
题目内容
在正项等差数列{an}中,a1=2,bn=an+n-1,且b1,b3,b9成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)令cn=
,设{bn}的前n项和为Tn,求f(n)=Tn+
(n∈N*)的最大值.
(1)求数列{an}、{bn}的通项公式;
(2)令cn=
| 1 |
| anbn |
| an |
| bn |
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)设{an}的公差为d,可表示an,bn,由b1,b3,b9成等比数列,有b1b9=b32,得关于d的方程,再由an>0,可得d=1,从而可得结果;
(2)利用裂项相消法可求得Tn=
,则f(n)=
+
=
(
+
),令t=
=1-
,易求t范围,由关于t的单调性可得最大值;
(2)利用裂项相消法可求得Tn=
| n |
| 2(n+1) |
| n |
| 2(n+1) |
| n+1 |
| 2n |
| 1 |
| 2 |
| n |
| n+1 |
| n+1 |
| n |
| n |
| n+1 |
| 1 |
| n+1 |
解答:
解:(1)设{an}的公差为d,则an=2+(n-1)d,bn=an+n-1=n+1+(n-1)d,
由b1,b3,b9成等比数列,有b1b9=b32,即2(8d+10)=(2d+4)2,得d2=1,
又an>0,故d=1,即an=n+1,bn=2n;
(2)cn=
=
=
(
-
),
故Tn=
(1-
+
-
+…+
-
)=
,
于是f(n)=
+
=
(
+
),
令t=
=1-
,则t是关于n的增函数,当n=1是,t=
,
故t∈[
,1),而g(t)=
(t+
)在t∈[
,1)上是减函数,
∴t=
,即n=1时,f(n)的最大值为
.
由b1,b3,b9成等比数列,有b1b9=b32,即2(8d+10)=(2d+4)2,得d2=1,
又an>0,故d=1,即an=n+1,bn=2n;
(2)cn=
| 1 |
| anbn |
| 1 |
| 2n(n+1) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
故Tn=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| 2(n+1) |
于是f(n)=
| n |
| 2(n+1) |
| n+1 |
| 2n |
| 1 |
| 2 |
| n |
| n+1 |
| n+1 |
| n |
令t=
| n |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 2 |
故t∈[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| t |
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
| 5 |
| 4 |
点评:本题考查等差数列、等比数列的通项公式及数列求和,考查函数思想,考查学生分析解决问题的能力,裂项相消法对数列求和是高考考查的重点内容,要使熟练.

练习册系列答案
相关题目
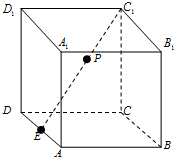 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )
如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|