题目内容
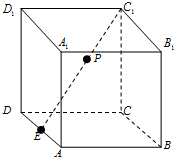 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )
如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:点、线、面间的距离计算
专题:计算题,转化思想,空间位置关系与距离
分析:如图所示,取A1D1的中点F,连接EF,EC1,利用线面平行的性质即可得到C1C∥平面D1EF,进而得到异面直线D1E与C1C的距离.
解答:
 解:如图所示,取A1D1的中点F,连接EF,EC1,
解:如图所示,取A1D1的中点F,连接EF,EC1,
∵EF∥CC1,EF=CC1=BB1,BB1⊥底面ABCD,
∴四边形EFB1B是矩形.
∴BB1∥EF,
又EF?平面C1EF,BB1?平面C1EF,∴BB1∥平面C1EF.
∴直线B1B上任一点到平面C1EF的距离是两条异面直线C1E与BB1的距离.
过点B1作B1M⊥C1F,
∵平面C1EF⊥平面A1B1C1D1.
∴B1M⊥平面C1EF.
过点M作MP∥EF交C1E于点P,则MP∥C1C.
取B1N=MP,连接PN,则四边形MPNB1是矩形.
可得NP⊥平面C1EF,
在△B1C1F中,B1M•C1F=B1C1•A1B1,又C1F=
=
,得B1M=
=
.
∴点P到直线CC1的距离的最小值为
.
故选:C.
 解:如图所示,取A1D1的中点F,连接EF,EC1,
解:如图所示,取A1D1的中点F,连接EF,EC1,∵EF∥CC1,EF=CC1=BB1,BB1⊥底面ABCD,
∴四边形EFB1B是矩形.
∴BB1∥EF,
又EF?平面C1EF,BB1?平面C1EF,∴BB1∥平面C1EF.
∴直线B1B上任一点到平面C1EF的距离是两条异面直线C1E与BB1的距离.
过点B1作B1M⊥C1F,
∵平面C1EF⊥平面A1B1C1D1.
∴B1M⊥平面C1EF.
过点M作MP∥EF交C1E于点P,则MP∥C1C.
取B1N=MP,连接PN,则四边形MPNB1是矩形.
可得NP⊥平面C1EF,
在△B1C1F中,B1M•C1F=B1C1•A1B1,又C1F=
AB2+(
|
| 10 |
| 3×2 | ||
|
3
| ||
| 5 |
∴点P到直线CC1的距离的最小值为
3
| ||
| 5 |
故选:C.
点评:本题考查异面直线的距离的求法,熟练掌握通过线面平行的性质即可得到异面直线的距离是解题的关键.考查转化思想的应用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知a=log45,b=4-
,c=sin2,则a、b、c的大小关系是( )
| 1 |
| 2 |
| A、b<c<a |
| B、c<a<b |
| C、a<b<c |
| D、c<b<a |
已知函数f(x)=
,则f(f(4))等于( )
|
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、2 |
已知角θ为第四象限角,且tanθ=-
,则sinθ+cosθ=( )
| 3 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2)的圆的方程是( )
| A、(x-1)2+(y+4)2=8 |
| B、(x-3)2+(y-1)2=9 |
| C、(x+1)2+(y-3)2=5 |
| D、(x-1)2+(y-5)2=16 |
在△ABC中,边a,b,c的对角分别为A,B,C,若a2=b2+c2+
bc,则A的大小为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知α,β均为锐角,且3sinα=2sinβ,3cosα+2cosβ=3,则α+2β的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |