Question

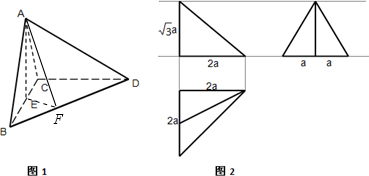
某几何体的直观图如图1，其按一定比例画出的三视图如图2，三视图中的长度a对应直观图中2cm．

（1）结合两个图形，试指出该几何体中相互垂直的面与相互垂直的线段，并指出相关线段的长度；
（2）求AB与CD所成角的大小：
（3）求二面角A-BD-C的平面角的正切值；
（4）计算该几何体的体积与表面积．

Answer 1

考点：由三视图求面积、体积,与二面角有关的立体几何综合题

专题：计算题,空间位置关系与距离

分析：（1）根据三视图的长、宽、高可判断BC、CD、AE长；根据、三视图的形状可判断平面ABC与平面BCD垂直；CD与平面ABC垂直，进而判断CD与BC、AC、AB垂直；
（2）利用证明AB⊥CD，可求AB与CD所成的角；
（3）过点E作EF⊥BD于F，连接AF，可证∠AFE即为所求二面角的平面角，在△AEF中，求tan∠AFE的大小；
（4）根据（1）中所得的数量及线线垂直关系，分别求出相关的量，代入面积与体积公式计算．

解答： 解：（1）三棱锥A-BCD中，面ABC⊥面BCD，
∠BCD=90°，∴BC⊥CD，CD⊥平面ABC，∵AC，AB?平面ABC，CD?平面ACD，
∴CD⊥AC，CD⊥AB，平面ACD⊥平面ABC
AC=CD=BC=AB=4，AE=2

3

，E为BC的中点；
（2）面ABC⊥面BCD，面ABC∩面BCD=BC，
∵CD⊥BC，∴CD⊥面ABC
∵AB?面ABC，∴CD⊥AB
即AB与CD所成的角是90°
（3）过点E作EF⊥BD于F，连接AF，则EF为AF在平面BCD内的射影，由三垂线定理得AF⊥BD，
∴∠AFE即为所求二面角的平面角，
AE=2

3

，在Rt△BEF中，∠EBF=45°，BE=2．
∴EF=

2

，∴tan∠AFE=

AE

EF

=

2 3

2

=

6

．
（4）由三视图可知AE=2

3

，且为三棱锥的高，
三棱锥A-BCD的体积为V=

1

3

•2

3

•

1

2

×4×4=

16

3

3

（cm³）
由（2）可知CD⊥AC，CD⊥BC
∴S_△ACD=S_△BCD=

1

2

×4×4=8；
S_△ABC=

1

2

×4×2

3

=4

3

；
△ABD中，AF=

AE2+EF2

=

12+2

=

14

，BD=4

2

，∴S△ABD=

1

2

×4×2

7

=4

7

∴S=8+8+4

3

+4

7

=（16+4

3

+4

7

）cm²

点评：本题考查了由三视图判断几何体中线面、线线、面面的垂直关系，求几何体的表面积与体积，考查了二面角的平面角的求法，
考查了学生的空间想象能力与运算能力，综合性强；解答的关键是由三视图正确判断几何量的大小及线面、面面、线线关系．