题目内容
4.已知M是关于x的不等式2x2+(3a-7)x+3+a-2a2<0解集,且M中的一个元素是0,求实数a的取值范围,并用a表示出该不等式的解集.分析 根据原不等式即(2x-a-1)(x+2a-3)<0,有一个元素是x=0,带入不等式,求出a的范围.对a讨论,表示出该不等式的解集.
解答 解:不等式2x2+(3a-7)x+3+a-2a2<0,因式分解,可得(2x-a-1)(x+2a-3)<0,
由方程(2x-a-1)(x+2a-3)=0,可得两个根分别为:x1=$\frac{a+1}{2}$,x2=3-2a.
由x=0适合不等式,
故得(a+1)(2a-3)>0,
∴a<-1,或a>$\frac{3}{2}$.
若a<-1,x1<x2,此时不等式的解集为{x|$\frac{a+1}{2}$<x<3-2a}.
若a>$\frac{3}{2}$,x1>x2,此时不等式的解集为{x|$\frac{a+1}{2}$>x>3-2a}.
(提示:利用作差比较x1,x2的大小)
点评 本题主要考查了一元二次不等式的应用,以及根与系数的关系,同时考查了分析求解的能力和计算能力,属于中档题.

练习册系列答案
相关题目
15.函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(2-x)>0的解集为( )
| A. | {x|-2<x<2} | B. | {x|x>2,或x<-2} | C. | {x|0<x<4} | D. | {x|x>4,或x<0} |
19.已知数列{an}的前n项和记为Sn,${S_n}=\frac{1}{3}({a_n}-1)(n∈{N^*})$,则an=( )
| A. | ${(-\frac{1}{2})^n}$ | B. | $-\frac{1}{2^n}$ | C. | $-{(-\frac{1}{2})^n}$ | D. | $-{(\frac{1}{2})^{n-1}}$ |
9.用数学归纳法证明n2<2n(n为自然数且n≥5)时,第一步应( )
| A. | 证明n=0时,n2<2n | B. | 证明n=5时,n2<2n | C. | 证明n=1时,n2<2n | D. | 证明n=6时,n2<2n |
14.已知函数$f(x)=\frac{1}{x}$,则f'(2)等于( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
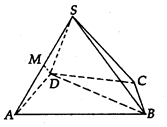 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.