题目内容
5.设A、B分别是复数z1、z2,在复平面上对应的两点,O为原点,若|z1+z2|=|z1-z2|,则∠AOB的大小为90°.分析 利用复数的几何意义,结合向量的性质进行判断即可.
解答 解:设复数z1、z2在复平面内对应的向量为$\overrightarrow{{Z}_{1}}$,$\overrightarrow{{Z}_{2}}$,
则由|z1+z2|=|z1-z2|,得|$\overrightarrow{{Z}_{1}}+\overrightarrow{{Z}_{2}}$|=|$\overrightarrow{{Z}_{1}}-\overrightarrow{{Z}_{2}}$|,
则以向量$\overrightarrow{{Z}_{1}}$,$\overrightarrow{{Z}_{2}}$为邻边的平行四边形为矩形,
则∠AOB的大小是90°,
故答案为:90°.
点评 本题主要考查复数几何意义的意义,根据条件转化为向量是解决本题的关键,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.正项等比数列{an}中,a1+a4+a7=2,a3+a6+a9=18,则{an}的前9项和S9=( )
| A. | 14 | B. | 26 | C. | 30 | D. | 29 |
20.已知函数f(x)=lnx-3x,则曲线y=f(x)在点(1,f(1))处的切线与坐标轴围成的三角形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
1.平面直角坐标系中,已知点A(1,-2),B(4,0),P(a,1),N(a+1,1),当四边形PABN的周长最小时,过三点A,P,N的圆的圆心坐标是( )
| A. | (3,-$\frac{9}{8}$) | B. | (3,-$\frac{7}{8}$) | C. | (5,-$\frac{9}{8}$) | D. | (4,-$\frac{5}{8}$) |
19.已知数列{an}的前n项和记为Sn,${S_n}=\frac{1}{3}({a_n}-1)(n∈{N^*})$,则an=( )
| A. | ${(-\frac{1}{2})^n}$ | B. | $-\frac{1}{2^n}$ | C. | $-{(-\frac{1}{2})^n}$ | D. | $-{(\frac{1}{2})^{n-1}}$ |

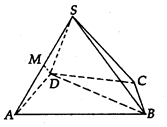 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.