题目内容
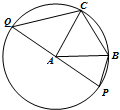
如图,PQ是半径为1的圆A的直径,△ABC是边长为1的正三角形,则
•
的最大值为 .
| BP |
| CQ |

考点:平面向量数量积的运算,向量在几何中的应用
专题:平面向量及应用
分析:利用向量的三角形法则、数量积运算即可得出.
解答:
解:由图可知
=
-
,
=
-
,
从而
•
=-1-
•
-
•
+
,
设∠BAP=θ,
则
•
=-cos(θ+60°)-cos(180°-θ)-
=sin(θ+30°)-
,
故当θ=60°时,
•
的最大值为
.
故答案为:
.
| BP |
| AP |
| AB |
| CQ |
| AQ |
| AC |
从而
| BP |
| CQ |
| AP |
| AC |
| AQ |
| AB |
| 1 |
| 2 |
设∠BAP=θ,
则
| BP |
| CQ |
| 1 |
| 2 |
| 1 |
| 2 |
故当θ=60°时,
| BP |
| CQ |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了向量的三角形法则、数量积运算、两角和差的正弦公式、三角函数的单调性,属于基础题.

练习册系列答案
相关题目
运行如图所示的程序框图,则输出的结果是( )


A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
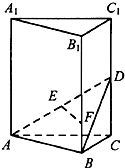 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
