题目内容
已知集合M={-2，2}，N={-2，0}，则M∩N（ ）
| A、{-2，0，2} |
| B、{-2，2} |
| C、{-2} |
| D、{0，2} |
考点：交集及其运算
专题：集合
分析：由M与N，求出两集合的交集即可．
解答：
解：∵M={-2，2}，N={-2，0}，
∴M∩N={-2}．
故选：C．
∴M∩N={-2}．
故选：C．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
若全集A={-1，0，1}，则集合A的子集共有（ ）
| A、3个 | B、5个 | C、7个 | D、8个 |
命题“?x0∈Q，sinx0+cosx0-2 Φ0≤0”的否定是（ ）
| A、?x0∉Q，sinx0+cosx0-2 Φ0≤0 |
| B、?x0∈Q，sinx0+cosx0-2 Φ0＞0 |
| C、?x∈Q，sinx+cosx-2Φ≤0 |
| D、?x∈Q，sinx+cosx-2Φ＞0 |
设集合M={x|y=
}，集合N={y|y=x2，x∈M}，则M∩N=（ ）
| x-2 |
| A、[2，+∞） |
| B、[4，+∞） |
| C、[0，+∞） |
| D、[0，4] |
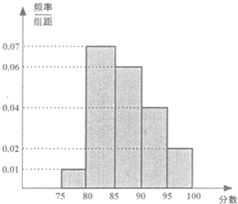一企业某次招聘新员工分笔试和面试两部分，人力资源部经理把参加笔试的40名学生的成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100），得到频率分布直方图如图所示．