题目内容
一个社会调查机构为了解某社区居民的月收入情况,从该社区成人居民中抽取10000人进行调查,根据所得信息制作了如图所示的样本频率分布直方图.

(Ⅰ)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,试求其中月收入在[2000,2500)(2000元至2500元之间)的人数;
(Ⅱ)为了估计从该社区任意抽取的3个居民中恰有2人月收入在[2000,3000)的概率P,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示月收入在[2000,3000)的居民,剩余的数字表示月收入不在[2000,3000)的居民;再以每三个随机数为一组,代表收入的情况.假设用上述随机模拟方法已产生了表中的20组随机数,请根据这批随机数估计概率P的值.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
(Ⅲ)任意抽取该社区的5位居民,用ξ表示月收入在[2000,3000)(元)的人数,求ξ的数学期望与方差.

(Ⅰ)为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,试求其中月收入在[2000,2500)(2000元至2500元之间)的人数;
(Ⅱ)为了估计从该社区任意抽取的3个居民中恰有2人月收入在[2000,3000)的概率P,特设计如下随机模拟的方法:先由计算器产生0到9之间取整数值的随机数,依次用0,1,2,3,…9的前若干个数字表示月收入在[2000,3000)的居民,剩余的数字表示月收入不在[2000,3000)的居民;再以每三个随机数为一组,代表收入的情况.假设用上述随机模拟方法已产生了表中的20组随机数,请根据这批随机数估计概率P的值.
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
(Ⅲ)任意抽取该社区的5位居民,用ξ表示月收入在[2000,3000)(元)的人数,求ξ的数学期望与方差.
考点:频率分布直方图,离散型随机变量的期望与方差
专题:概率与统计
分析:(I)由频率分布直方图先算出月收入在[2000,2500)的频率v,即可得出应抽取的人数=100v;
(II)由频率分布直方图可知,月收入在[2000,3000)的频率为0.4,因此 可以用数字0,1,2,3表示收入在[2000,3000)的居民,数字4,5,6,7,8,9表示月收入不在[2000,3000)的居民,再观察上述随机数得出要求的事件包括的基本事件的个数,再利用古典概型的定义即可得出;
(III)利用二项分布列的计算公式即可得出.
(II)由频率分布直方图可知,月收入在[2000,3000)的频率为0.4,因此 可以用数字0,1,2,3表示收入在[2000,3000)的居民,数字4,5,6,7,8,9表示月收入不在[2000,3000)的居民,再观察上述随机数得出要求的事件包括的基本事件的个数,再利用古典概型的定义即可得出;
(III)利用二项分布列的计算公式即可得出.
解答:
解:(Ⅰ)由频率分布直方图可知:月收入在[2000,2500)的频率=0.0002×500=0.1,
∴应抽取的人数为0.1×100=10人.
(Ⅱ)由频率分布直方图可知,月收入在[2000,3000)的频率=0.0002×500+0.0006×500=0.4
∴可以用数字0,1,2,3表示收入在[2000,3000)的居民,数字4,5,6,7,8,9表示月收入不在[2000,3000)的居民;
观察上述随机数可得,该社区3个居民中恰有2个月收入在[2000,3000)的有191,271,932,812,431,393,027,730,共有8个.
而基本事件一共有20个,根据古典概型的定义可知该社区3个居民中恰有2个月收入在[2000,3000)的概率为P=
=0.4.
(Ⅲ)由频率分布直方图可知,任意抽取该社区1位居民,月收入在[2000,3000)(元)的概率为0.4,
∴随机变量ξ服从B(5,0.4),
∴Eξ=5×0.4=2,Dξ=5×0.4×(1-0.4)=1.2.
∴应抽取的人数为0.1×100=10人.
(Ⅱ)由频率分布直方图可知,月收入在[2000,3000)的频率=0.0002×500+0.0006×500=0.4
∴可以用数字0,1,2,3表示收入在[2000,3000)的居民,数字4,5,6,7,8,9表示月收入不在[2000,3000)的居民;
观察上述随机数可得,该社区3个居民中恰有2个月收入在[2000,3000)的有191,271,932,812,431,393,027,730,共有8个.
而基本事件一共有20个,根据古典概型的定义可知该社区3个居民中恰有2个月收入在[2000,3000)的概率为P=
| 8 |
| 20 |
(Ⅲ)由频率分布直方图可知,任意抽取该社区1位居民,月收入在[2000,3000)(元)的概率为0.4,
∴随机变量ξ服从B(5,0.4),
∴Eξ=5×0.4=2,Dξ=5×0.4×(1-0.4)=1.2.
点评:本题综合考查了频率分布直方图的有关知识、古典概型的计算公式、二项分布列、分层抽样等在基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
已知集合A={x|x2-11x+10≤0},B={y|y=lgx,x∈A},则A∪B=( )
| A、[0,1] |
| B、[1,10] |
| C、{1} |
| D、[0,10] |
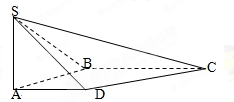 在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=
在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=