题目内容
 已知向量
已知向量| m |
| ωx |
| 2 |
| ||
| 3 |
| n |
| ωx |
| 2 |
| 3 |
| m |
| n |
(1)求ω的值及函数f(x)的值域;
(2)若0<ω<1,当f(x0)=-
4
| ||
| 3 |
| 14 |
| 3 |
| 8 |
| 3 |
考点:平面向量数量积的运算,正弦函数的图象,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(1)利用向量的数量积运算和三角函数的二倍角公式,化简得到f(x),再有函数的图象,求出ω的值和函数的值域
(2)由(1)得到函数的解析式,再利用两角和的正余弦公式求出f(x0+1)的值.
(2)由(1)得到函数的解析式,再利用两角和的正余弦公式求出f(x0+1)的值.
解答:
解:(1)f(x)=
•
=2cos2
+
sinωx-1=
sinωx+cosωx=2sin(ωx+
)

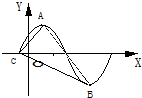
由对称性可知AB必过f(x)的零点D,
如果角A为直角,则△ACD为等腰直角三角形,高为2
故CD=4,即函数f(x)的周期T=2×4=8,所以
=8⇒ω=
如果角C为直角,CD=
AB,即
=
⇒T=
,ω=
综上,ω的值为
或
,函数f(x)的值域为[-2,2].…(6分)
(2)因为0<ω<1,所以ω=
,即f(x)=2sin(
x+
)
∵f(x0)=-
∴2sin(
x0+
)=-
,
即sin(
x0+
)=-
…(8分)
由x0∈[-
,-
],
可得
x0+
∈[-π,-
],
所以cos(
x0+
)=-
…(10分)
f(x0+1)=2sin[(
x0+
)+
]
=2sin[(
x0+
)cos
+cos[(
x0+
)sin
]
=2(-
×
-
×
)=-
…(12分)
| m |
| n |
| ωx |
| 2 |
| 3 |
| 3 |
| π |
| 6 |

由对称性可知AB必过f(x)的零点D,
如果角A为直角,则△ACD为等腰直角三角形,高为2
故CD=4,即函数f(x)的周期T=2×4=8,所以
| 2π |
| ω |
| π |
| 4 |
如果角C为直角,CD=
| 1 |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
(
|
| 8 |
| 3 |
| 3 |
| ||
| 4 |
综上,ω的值为
| π |
| 4 |
| ||
| 4 |
(2)因为0<ω<1,所以ω=
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
∵f(x0)=-
4
| ||
| 3 |
| π |
| 4 |
| π |
| 6 |
4
| ||
| 3 |
即sin(
| π |
| 4 |
| π |
| 6 |
2
| ||
| 3 |
由x0∈[-
| 14 |
| 3 |
| 8 |
| 3 |
可得
| π |
| 4 |
| π |
| 6 |
| π |
| 2 |
所以cos(
| π |
| 4 |
| π |
| 6 |
| 1 |
| 3 |
f(x0+1)=2sin[(
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
=2sin[(
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
=2(-
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
4+
| ||
| 3 |
点评:本题主要考察三角函数的图象与性质、同角三角函数的关系、两角和的正余弦公式、两倍角公式等基础知识,考查运算能力,数形结合、整体转化等数学思想,三角函数以向量为载体的形式给出,在三角函数图象中巧妙嵌入直角三角形,活而不难、平中见奇.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
集合A={(x,y)|y=ax+1},B={(x,y)|y=x+3},且A∩B={(2,5)},则( )
| A、a=3 | B、a=2 |
| C、a=-3 | D、a=-2 |
已知向量
=(2,1)和
=(x-1,y)垂直,则|
+
|的最小值为( )
| a |
| b |
| a |
| b |
A、
| ||
| B、5 | ||
C、2
| ||
D、
|
在△ABC中,a=5,b=8,C=60°,则
•
的值为( )
| CA |
| CB |
| A、-20 | ||
| B、20 | ||
C、20
| ||
D、-20
|
