题目内容
已知函数f(x)=ax+lnx,其中为常数.
(Ⅰ)当a=-1时,求f(x)的单调增区间;
(Ⅱ)当0<-
<e时,若f(x)在区间(0,e)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,试推断方程|f(x)|=
+
是否有实数根.
(Ⅰ)当a=-1时,求f(x)的单调增区间;
(Ⅱ)当0<-
| 1 |
| a |
(Ⅲ)当a=-1时,试推断方程|f(x)|=
| lnx |
| x |
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,综合题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)先求函数f(x)的定义域为{x|x>0},再代入求导f′(x)=
,从而确定函数的单调区间;
(Ⅱ)令f′(x)=a+
=0解得x=-
;从而确定单调性及最值及即可;
(Ⅲ)由(Ⅰ)知当a=-1时,f(x)max=f(1)=-1,从而得|f(x)|≥1;再令g(x)=
+
,则g′(x)=
;从而求最值即可.
| 1-x |
| x |
(Ⅱ)令f′(x)=a+
| 1 |
| x |
| 1 |
| a |
(Ⅲ)由(Ⅰ)知当a=-1时,f(x)max=f(1)=-1,从而得|f(x)|≥1;再令g(x)=
| lnx |
| x |
| 1 |
| 2 |
| 1-lnx |
| x2 |
解答:
解:(Ⅰ)由已知知函数f(x)的定义域为{x|x>0},
当a=-1时,f(x)=-x+lnx,f′(x)=
;
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0;
所以,f(x)的单调增区间为(0,1).
(Ⅱ)因为f′(x)=a+
,
令f′(x)=0解得x=-
;
由f′(x)>0解得0<x<-
,由f′(x)<0解得-
<x<e;
从而f(x)的单调增区间为(0,-
),减区间为(-
,e);
所以,f(x)max=f(-
)=-1+ln(-
)=-3;
解得,a=-e2.
(Ⅲ)由(Ⅰ)知当a=-1时,f(x)max=f(1)=-1,
所以,|f(x)|≥1;
令g(x)=
+
,则g′(x)=
;
当0<x<e时,g′(x)>0;当x>e时,g′(x)<0;
从而g(x)在(0,e)上单调递增,在(e,+∞)上单调递减;
所以,g(x)max=g(e)=
+
<1;
所以,|f(x)|>g(x),
即|f(x)|>
+
;
所以,方程|f(x)|=
+
没有实数根.
当a=-1时,f(x)=-x+lnx,f′(x)=
| 1-x |
| x |
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0;
所以,f(x)的单调增区间为(0,1).
(Ⅱ)因为f′(x)=a+
| 1 |
| x |
令f′(x)=0解得x=-
| 1 |
| a |
由f′(x)>0解得0<x<-
| 1 |
| a |
| 1 |
| a |
从而f(x)的单调增区间为(0,-
| 1 |
| a |
| 1 |
| a |
所以,f(x)max=f(-
| 1 |
| a |
| 1 |
| a |
解得,a=-e2.
(Ⅲ)由(Ⅰ)知当a=-1时,f(x)max=f(1)=-1,
所以,|f(x)|≥1;
令g(x)=
| lnx |
| x |
| 1 |
| 2 |
| 1-lnx |
| x2 |
当0<x<e时,g′(x)>0;当x>e时,g′(x)<0;
从而g(x)在(0,e)上单调递增,在(e,+∞)上单调递减;
所以,g(x)max=g(e)=
| 1 |
| e |
| 1 |
| 2 |
所以,|f(x)|>g(x),
即|f(x)|>
| lnx |
| x |
| 1 |
| 2 |
所以,方程|f(x)|=
| lnx |
| x |
| 1 |
| 2 |
点评:本题考查了导数的综合应用及存在性命题的处理方法,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 已知正方形ABCD的边长为2
已知正方形ABCD的边长为2



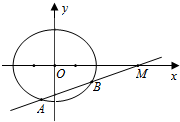 如图所示,椭圆C:
如图所示,椭圆C: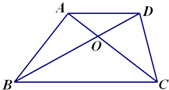 如图:在梯形ABCD中,AD∥BC且
如图:在梯形ABCD中,AD∥BC且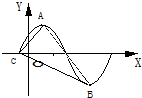 已知向量
已知向量