题目内容
10．如图是一个空间几何体的三视图，则该几何体体积是（ ）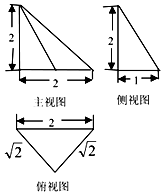
| A． | $\frac{1}{3}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | $\frac{2}{3}$ |
分析 由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，代入锥体体积公式，可得答案．
解答 解：由已知中的三视图可得该几何体是一个以俯视图为底面的三棱锥，
其底面是一个等腰直角三角形，故S=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1，
高h=2，
故体积V=$\frac{1}{3}Sh$=$\frac{2}{3}$，
故选：D
点评 本题考查的知识点是棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
1．
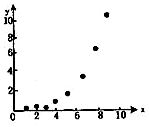如图所示的散点图，现选用两种回归模型，模型A：使用线性回归，计算相关指数$R_1^2$；模型B：用指数回归，计算出相关指数$R_2^2$，则一定有（ ）
如图所示的散点图，现选用两种回归模型，模型A：使用线性回归，计算相关指数$R_1^2$；模型B：用指数回归，计算出相关指数$R_2^2$，则一定有（ ）| A． | $R_1^2＞R_2^2$ | B． | $R_1^2＜R_2^2$ | C． | $R_1^2=R_2^2$ | D． | 无法确定 |
18．在△ABC中，角A，B，C所对的三边分别是a，b，c，已知$A={30°}，c=2\sqrt{3}，b=2$，则△ABC的面积为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
5．抛物线C：y2=2px（p＞0）的焦点与圆F：x2+y2-4x=0的圆心重合，点A，B，C在该抛物线上，且点F是△ABC的重心，则|FA|+|FB|+|FC|的值是（ ）
| A． | 6 | B． | 8 | C． | 9 | D． | 12 |
20．在三角形ABC中，三个内角A，B，C所对的边分别为a，b，c，若acosA=bcosB，则三角形ABC一定是（ ）三角形．
| A． | 直角 | B． | 等边 | C． | 钝角 | D． | 等腰或直角 |