Question

在半径为R的球内有一内接圆柱，设该圆柱底面半径为r，则圆柱侧面积最大时，

r

R

为（　　）

• A、

  1

  4

• B、

  1

  2

• C、

  2

  2

• D、

  3

  2

Answer 1

考点：球内接多面体

专题：计算题,空间位置关系与距离

分析：由题意圆柱的底面为球的截面，由球的截面性质可得出圆柱的高为h、底面半径为r与球的半径为R的关系，再用h和r表示出圆柱的侧面积，利用基本不等式求最值即可．

解答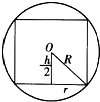： 解：如图为轴截面，令圆柱的高为h，底面半径为r，侧面积为S，
则（

h

2

）²+r²=R²，
即h=2

R2-r2

．
∵S=2πrh=4πr•

R2-r2

≤4π

(r2+R2-r2)2 2

=2πR²，
取等号时，内接圆柱底面半径为

2

2

R，
∴

r

R

=

2

2

．
故选：C．

点评：本题考查球与圆柱的组合体问题、以及利用基本不等式求最值问题，难度一般．