题目内容
函数f(x)=
,若f(x)≥4,则x的取值范围为 .
|
考点:指数函数单调性的应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:讨论当x≥1时,当x<1时,分别解指数不等式和二次不等式,再求并集即可.
解答:
解:当x≥1时,f(x)≥4即为2x≥4,解得x≥2,则有x≥2;
当x<1时,f(x)≥4即为(x-1)2≥4,解得x≥3或x≤-1,则有x≤-1.
综上可得,x的取值范围是x≤-1,或x≥2.
故答案为:(-∞,-1]∪[2,+∞).
当x<1时,f(x)≥4即为(x-1)2≥4,解得x≥3或x≤-1,则有x≤-1.
综上可得,x的取值范围是x≤-1,或x≥2.
故答案为:(-∞,-1]∪[2,+∞).
点评:本题考查分段函数的运用:解不等式,考查指数不等式和二次不等式的解法,考查运算能力,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
古希腊数学家把数1,3,6,10,15,21…叫作三角形数,它们有一定的规律性,则第22个三角形数为( )
| A、210 | B、276 |
| C、231 | D、253 |
设动点C到点M(0,3)的距离与到直线y=-3的距离相等,则动点C的轨迹是( )
| A、抛物线 | B、双曲线 | C、椭圆 | D、圆 |
为了检验中学生眼睛近视是否与性别有关时用什么方法最有说服力( )
| A、平均数 | B、方差 |
| C、回归分析 | D、独立性检验 |
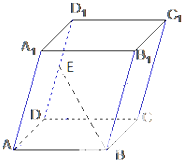 如图,在平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=4,∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点,设
如图,在平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=4,∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点,设