题目内容
19.设命题p:?x0∈(-2,+∞),6+|x0|=5,命题q:?x∈(-∞,0),x2+$\frac{4}{{x}^{2}}$≥4.命题r:若a≥1,则函数f(x)=ax+cosx(x∈R)是增函数.(1)写出命题r的否命题;
(2)判断命题¬p:p∨r,p∧q的真假,并说明理由.
分析 (1)根据否命题的定义,否定题设也否定结论,求出r的否命题即可;
(2)根据原命题的真假判断复合命题的真假即可.
解答 解:(1)命题r:若a≥1,则函数f(x)=ax+cosx(x∈R)是增函数,
则命题r的否命题是:若a<1,则函数f(x)=ax+cosx(x∈R)不是增函数;
(2)命题p:?x0∈(-2,+∞),6+|x0|=5,是假命题;
命题q:?x∈(-∞,0),x2+$\frac{4}{{x}^{2}}$≥2$\sqrt{4}$=4,当且仅当x=-$\sqrt{2}$时“=”成立,
故命题q是真命题;
对于f(x)=ax+cosx,a≥1,f′(x)=a-sinx≥a-1≥0,
故命题r:若a≥1,则函数f(x)=ax+cosx(x∈R)是增函数,是真命题;
故命题¬p是真命题,
p∨r是真命题,p∧q是假命题.
点评 本题考查了复合命题的判断,考查否命题的定义,是一道中档题.

练习册系列答案
相关题目
14.“a≤0”是“函数f(x)=ax+lnx存在极值”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
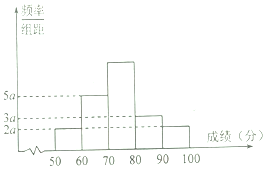 某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.
某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.