题目内容
4.已知三棱锥A-BCD中,AD⊥平面BCD,AD=BD=CD=1,E是BC中点,则直线AE与CD所成角的余弦值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{3\sqrt{2}}{8}$ |
分析 以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,利用向量法能求出直线AE与CD所成角的余弦值.
解答 解: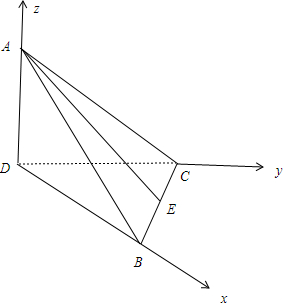 以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,
以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,
A(0,0,1),B(1,0,0),C(0,1,0),E($\frac{1}{2},\frac{1}{2}$,0),D(0,0,0),
$\overrightarrow{AE}$=($\frac{1}{2},\frac{1}{2}$,-1),$\overrightarrow{CD}$=(0,-1,0),
设直线AE与CD所成角为θ,
则直线AE与CD所成角的余弦值为:
cosθ=$\frac{|\overrightarrow{AE}•\overrightarrow{CD}|}{|\overrightarrow{AE}|•|\overrightarrow{CD}|}$=$\frac{\frac{1}{2}}{\sqrt{\frac{6}{4}}}$=$\frac{\sqrt{6}}{6}$.
故选:C.
点评 本题考查异面直线所成角的大小的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
15.函数f(x)=(x2+ax-1)ex的一个极值点为x=1,则f(x)的极大值为( )
| A. | -1 | B. | -2e-2 | C. | 5e-2 | D. | 1 |
12.由下列各组命题构成的复合命题中,“p 或 q”为真,“p 且 q”为假,“非 p”为真的一组为( )
| A. | p:3 为偶数,q:4 为奇数 | B. | p:π<3,q:5>3 | ||
| C. | p:a∈{a,b},q:{a}⊆{a,b} | D. | p:Q⊆R,q:N=Z |
19.$\frac{1-{i}^{3}}{1-i}$=( )
| A. | -i | B. | i | C. | 1+i | D. | 1 |
 某市重点中学奥数培训班共有15人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,甲组学生成绩的极差是m,乙组学生成绩的中位数是86,则m+n的值是21.
某市重点中学奥数培训班共有15人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,甲组学生成绩的极差是m,乙组学生成绩的中位数是86,则m+n的值是21.