题目内容
17.设集合A={x∈N|,0≤x≤2},B={x∈N|1≤x≤3},则A∪B=( )| A. | {1,2} | B. | {0,1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
分析 化简集合A、B,根据并集的定义写出A∪B.
解答 解:集合A={x∈N|,0≤x≤2}={0,1,2},
B={x∈N|1≤x≤3}={1,2,3},
则A∪B={0,1,2,3}.
故选:B.
点评 本题考查了集合的化简与运算问题,是基础题.

练习册系列答案
相关题目
8. 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
5.在等比数列{an}中,若a1=2,a4=16,则{an}的前5项和S5等于( )
| A. | 30 | B. | 31 | C. | 62 | D. | 64 |
9.某超市计划每天购进某商品若干件,该超市每销售一件该商品可获利润80元,若供大于求,剩余商品全部退回,但每件商品亏损20元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量n(单位:件,n∈N),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间[800,900]内的概率.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量n(单位:件,n∈N),整理得下表:
| 日需求量 | 7 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 5 | 7 | 10 | 14 | 10 | 4 |
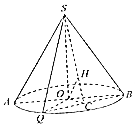 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.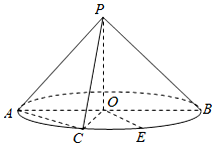 如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO=2$\sqrt{2}$.