题目内容
2.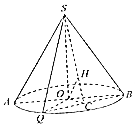 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.(Ⅰ)如果BQ的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(Ⅱ)如果∠AOQ=60°,QB=2$\sqrt{3}$,设二面角A-SB-Q的大小为θ,求cosθ的值.
分析 (Ⅰ)连结OC、AQ,推导出OC∥AQ,OC⊥BQ,SO⊥BQ,从而QB⊥平面SOC,进而OH⊥BQ,由此能证明OH⊥平面SBQ.
(Ⅱ)以O为原点,OA为x轴,在平面ABC内过O作AB的垂线为y轴,OS为z轴,建立空间直角坐标系,利用向量法能求出cosθ.
解答 证明:(Ⅰ)连结OC、AQ,
∵O为AB的中点,BQ的中点为C,
∴OC∥AQ,
∵AB为圆的直径,∠AQB=90°,∴OC⊥BQ,
∵SO⊥平面ABQ,SO⊥BQ,QB⊥平面SOC,
OH⊥BQ,
∴OH⊥平面SBQ.
解:(Ⅱ)由已知得QC=$\sqrt{3}$,OQ=2,OC=1,SO=2$\sqrt{3}$,
以O为原点,OA为x轴,在平面ABC内过O作AB的垂线为y轴,
OS为z轴,建立空间直角坐标系,
则A(2,0,0),B(-2,0,0),S(0,0,2$\sqrt{3}$),Q(1,$\sqrt{3}$,0),
$\overrightarrow{BS}$=(2,0,2$\sqrt{3}$),$\overrightarrow{BQ}$=(3,$\sqrt{3}$,0),
设$\overrightarrow{n}$=(x,y,z)为平面的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BS}=2x+2\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{BQ}=3x+\sqrt{3}y=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}$=(-$\sqrt{3}$,3,1),
而平面SAB的法向量$\overrightarrow{m}$=(0,1,0),
∴cosθ=$\frac{3}{\sqrt{13}}$=$\frac{3\sqrt{13}}{13}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

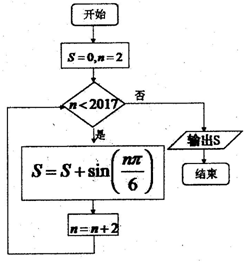
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
| A. | p | B. | (¬p)∧(¬q) | C. | q | D. | (¬p)∨(¬q) |
| A. | {1,2} | B. | {0,1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
| A. | $\frac{m+1}{m-1}$ | B. | $\frac{m-1}{m}$ | C. | $\frac{m-1}{m+1}$ | D. | $\frac{m}{m-1}$ |