题目内容
 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=4,BC=2,PA=
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=4,BC=2,PA=| 6 |
考点:直线与平面所成的角
专题:空间角
分析:以C为原点,CA为x轴,CB为y轴,建立空间直角坐标系,利用向量法能求出直线AB与平面PBC所成角的大小.
解答:
 解:以C为原点,CA为x轴,CB为y轴,建立空间直角坐标系,
解:以C为原点,CA为x轴,CB为y轴,建立空间直角坐标系,
由题意得A(0,2
,0),B(2,0,0),
C(0,0,0),P(0,2
,
),
=(2,-2
,0),
(0,2
,
),
=(2,0,0),
设平面PBC的法向量
=(x,y,z),
则
,
取x=
,得
=(0,
,-2),
设直线AB与平面PBC所成角为θ,
sinθ=|cos<
,
>|=|
|=
,
∴θ=30°.
故答案为:30°.
 解:以C为原点,CA为x轴,CB为y轴,建立空间直角坐标系,
解:以C为原点,CA为x轴,CB为y轴,建立空间直角坐标系,由题意得A(0,2
| 3 |
C(0,0,0),P(0,2
| 3 |
| 6 |
| AB |
| 3 |
| CP |
| 3 |
| 6 |
| CB |
设平面PBC的法向量
| n |
则
|
取x=
| 2 |
| n |
| 2 |
设直线AB与平面PBC所成角为θ,
sinθ=|cos<
| n |
| AB |
-2
| ||
4
|
| 1 |
| 2 |
∴θ=30°.
故答案为:30°.
点评:本题考查直线与平面所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
假设△ABC为圆的内接正三角形,向该圆内投一点,则点落在△ABC内的概率( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式16x-logax<0在(0,
)恒成立,则实数a的取值范围( )
| 1 |
| 4 |
A、(
| ||
B、(
| ||
C、[
| ||
D、[
|
用秦九韶算法计算当x=10时,f(x)=3x4+2x2+x+4的值的过程中,v1的值为( )
| A、30 | B、40 | C、35 | D、45 |
下列说法中正确的是( )
| A、平面内与两个定点的距离和等于正的常数的点的轨迹叫做椭圆 |
| B、不等式ax-b>0的解集为(1,+∞)的充要条件是:a=b |
| C、“若 a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
| D、一个命题的否命题为真,则它的逆命题一定为真 |
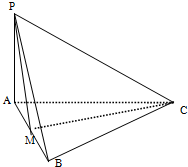 如图所示,PA⊥平面ABC,PA=AB,AB⊥BC,M为AB中点.
如图所示,PA⊥平面ABC,PA=AB,AB⊥BC,M为AB中点.